Ελκτική δύναμη ηλεκτρομαγνητών

Η δύναμη με την οποία ένας ηλεκτρομαγνήτης έλκει σιδηρομαγνητικά υλικά εξαρτάται από τη μαγνητική ροή F ή, ισοδύναμα, από την επαγωγή B και την περιοχή διατομής του ηλεκτρομαγνήτη S.

Η δύναμη πίεσης του ηλεκτρομαγνήτη καθορίζεται από τον τύπο

F = 40550 ∙ B ^ 2 ∙ S,

όπου F είναι η δύναμη πίεσης του ηλεκτρομαγνήτη, kg (η δύναμη μετριέται επίσης σε newton, 1 kg = 9,81 N ή 1 N = 0,102 kg). Β — επαγωγή, Τ; S είναι η περιοχή διατομής του ηλεκτρομαγνήτη, m2.

Παραδείγματα του

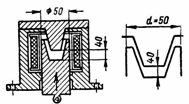
1. Ο ηλεκτρομαγνήτης της βρύσης είναι ένα μαγνητικό κύκλωμα (Εικ. 1). Ποια είναι η δύναμη ανύψωσης ενός ηλεκτρομαγνήτη πεταλογερανού, εάν η μαγνητική επαγωγή είναι B = 1 T και η περιοχή διατομής κάθε πόλου του ηλεκτρομαγνήτη είναι S = 0,02 m2 (Εικ. 1, β); Παραμελήστε την επίδραση του κενού μεταξύ του ηλεκτρομαγνήτη και του οπλισμού.

Ρύζι. 1. Ηλεκτρομαγνήτης ανύψωσης

F = 40550 ∙ B ^ 2 ∙ S; F = 40550 ∙ 1 ^ 2 ∙ 2 ∙ 0,02 = 1622 kg.

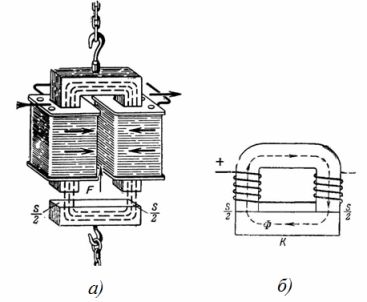
2. Ένας κυκλικός ηλεκτρομαγνήτης από χάλυβα έχει τις διαστάσεις που φαίνονται στο σχ. 2, α και β. Η ανυψωτική δύναμη του ηλεκτρομαγνήτη είναι 3 Τ. Προσδιορίστε την περιοχή διατομής του πυρήνα του ηλεκτρομαγνήτη, n. σ. και ο αριθμός των στροφών του πηνίου σε ρεύμα μαγνήτισης I = 0,5 A.

Ρύζι. 2. Στρογγυλός ηλεκτρομαγνήτης

Η μαγνητική ροή διέρχεται από τον κυκλικό εσωτερικό πυρήνα και επιστρέφει μέσω του κυλινδρικού σώματος. Οι περιοχές διατομής του πυρήνα Sc και του περιβλήματος Sk είναι περίπου οι ίδιες, επομένως οι τιμές επαγωγής στον πυρήνα και στο περίβλημα είναι πρακτικά οι ίδιες:

Sc = (π ∙ 40 ^ 2) / 4 = (3,14 ∙ 1600) / 4 = 1256 cm2 = 0,1256 m2,

Sk = ((72 ^ 2-60 ^ 2) ∙ π) / 4 = 3,14 / 4 ∙ (5184-3600) = 1243,5 cm2 = 0,12435 m2;

S = Sc + Sk = 0,24995 m2 ≈0,25 m2.

Η απαιτούμενη επαγωγή στον ηλεκτρομαγνήτη προσδιορίζεται από τον τύπο F = 40550 ∙ B ^ 2 ∙ S,

όπου B = √ (F / (40550 ∙ S)) = √ (3000 / (40550 ∙ 0,25)) = 0,5475 T.

Η τάση σε αυτή την επαγωγή βρίσκεται στην καμπύλη μαγνήτισης του χυτού χάλυβα:

H = 180 A / m.

Το μέσο μήκος της γραμμής πεδίου (Εικ. 2, β) lav = 2 ∙ (20 + 23) = 86 cm = 0,86 m.

Μαγνητική δύναμη I ∙ ω = H ∙ lav = 180 ∙ 0,86 = 154,8 Av; I = (I ∙ ω) / I = 154,8 / 0,5 = 310 A.

Στην πραγματικότητα n. s, δηλαδή το ρεύμα και ο αριθμός των στροφών, πρέπει να είναι πολλές φορές μεγαλύτεροι, αφού υπάρχει αναπόφευκτο διάκενο αέρα μεταξύ του ηλεκτρομαγνήτη και του οπλισμού, το οποίο αυξάνει σημαντικά τη μαγνητική αντίσταση του μαγνητικού κυκλώματος. Επομένως, το διάκενο αέρα πρέπει να λαμβάνεται υπόψη κατά τον υπολογισμό των ηλεκτρομαγνητών.

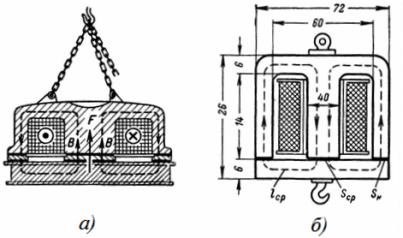
3. Το πηνίο του ηλεκτρομαγνήτη για τη βρύση έχει 1350 στροφές, το διαρρέει ρεύμα Ι = 12 Α. Οι διαστάσεις του ηλεκτρομαγνήτη φαίνονται στο σχ. 3. Τι βάρος σηκώνει ο ηλεκτρομαγνήτης σε απόσταση 1 cm από τον οπλισμό και τι βάρος μπορεί να κρατήσει μετά τη βαρύτητα;

Ρύζι. 3. Ηλεκτρομαγνητικό πηνίο

Το μεγαλύτερο μέρος του Ν. με I ∙ ω δαπανάται για τη διεξαγωγή μαγνητικής ροής μέσω του διακένου αέρα: I ∙ ω≈Hδ ∙ 2 ∙ δ.

Μαγνητική δύναμη I ∙ ω = 12 ∙ 1350 = 16200 A.

Αφού H ∙ δ = 8 ∙ 10 ^ 5 ∙ B, τότε Hδ ∙ 2 ∙ δ = 8 ∙ 10 ^ 5 ∙ B ∙ 0,02.

Επομένως, 16200 = 8 ∙ 10 ^ 5 ∙ B ∙ 0,02, δηλ. Β = 1,012 Τ.

Υποθέτουμε ότι η επαγωγή είναι B = 1 T, αφού μέρος του n. γ. Το I ∙ ω δαπανάται για την αγωγή της μαγνητικής ροής στον χάλυβα.

Ας ελέγξουμε αυτόν τον υπολογισμό με τον τύπο I ∙ ω = Hδ ∙ 2 ∙ δ + Hс ∙ lс.

Το μέσο μήκος της μαγνητικής γραμμής είναι: lav = 2 ∙ (7 + 15) = 44 cm = 0,44 m.

Η ένταση Hc σε B = 1 T (10000 Gs) προσδιορίζεται από την καμπύλη μαγνήτισης:

Hc = 260 A / m. I ∙ ω = 0,8 ∙ B ∙ 2 + 2,6 ∙ 44 = 1,6 ∙ 10000 + 114,4 = 16114 Av.

Η δύναμη μαγνήτισης I ∙ ω = 16114 Av που δημιουργεί μια επαγωγή B = 1 T είναι πρακτικά ίση με το δεδομένο n. v. I ∙ ω = 16200 Av.

Η συνολική επιφάνεια διατομής του πυρήνα και του κώνου είναι: S = 6 ∙ 5 + 2 ∙ 5 ∙ 3 = 0,006 m2.

Ο ηλεκτρομαγνήτης θα προσελκύσει φορτίο βάρους F = 40550 ∙ B ^ 2 ∙ S = 40550 ∙ 1 ^ 2 ∙ 0,006 = 243,3 kg από απόσταση 1 cm.

Δεδομένου ότι το διάκενο αέρα πρακτικά εξαφανίζεται μετά την έλξη του οπλισμού, ο ηλεκτρομαγνήτης μπορεί να αντέξει πολύ μεγαλύτερο φορτίο. Στην περίπτωση αυτή, ολόκληρο το ν. γ. Το I ∙ ω δαπανάται για την αγωγή της μαγνητικής ροής μόνο στον χάλυβα, επομένως I ∙ ω = Hс ∙ lс; 16200 = Hs ∙ 44; Hc = 16200/44 = 368 A/cm = 36800 A/m.

Σε μια τέτοια τάση, ο χάλυβας είναι πρακτικά κορεσμένος και η επαγωγή σε αυτό είναι περίπου 2 Τ. Ο ηλεκτρομαγνήτης έλκει τον οπλισμό με δύναμη F = 40550 ∙ B ^ 2 ∙ S = 40550 ∙ 4 ∙ 0,006 = 973 kg.

4. Το ρελέ σήματος αποτελείται από έναν θωρακισμένο ηλεκτρομαγνήτη 1 με στρογγυλό πυρήνα και οπλισμό τύπου βαλβίδας 2, ο οποίος, αφού τροφοδοτήσει ρεύμα στον ηλεκτρομαγνήτη, έλκει και απελευθερώνει το φλας 3, το οποίο ανοίγει το ψηφίο σήματος (Εικ. 4).

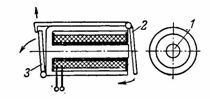
Ρύζι. 4. Ηλεκτρομαγνήτης θωράκισης

Η ισχύς μαγνήτισης είναι I ∙ ω = 120 Av, το διάκενο αέρα είναι δ = 0,1 cm και η συνολική επιφάνεια διατομής του ηλεκτρομαγνήτη είναι S = 2 cm2. Υπολογίστε τη δύναμη έλξης του ρελέ.

Η επαγωγή Β προσδιορίζεται με διαδοχικές προσεγγίσεις χρησιμοποιώντας την εξίσωση I ∙ ω = Hс ∙ lс + Hδ ∙ 2 ∙ δ.

Έστω n. γ. Hc ∙ lc είναι 15% I ∙ ω, δηλ. 18 Av.

Τότε I ∙ ω-Hс ∙ lс = Hδ ∙ 2 ∙ δ; 120-18 = Hδ ∙ 0,2; Hδ = 102 / 0,2 = 510 A / cm = 51000 A / m.

Βρίσκουμε λοιπόν την επαγωγή Β:

Hδ = 8 ∙ 10 ^ 5 V; B = Hδ / (8 ∙ 10 ^ 5) = 51000 / (8 ∙ 10 ^ 5) = 0,0637 T.

Αφού αντικαταστήσουμε την τιμή B στον τύπο F = 40550 ∙ B ^ 2 ∙ S, έχουμε:

F = 40550 ∙ 0,0637 ^ 2 ∙ 0,0002 = 0,0326 kg.

5. Η ηλεκτρομαγνητική βαλβίδα φρένου DC (Εικ. 5) έχει οπλισμό εμβόλου με κωνικό στοπ. Η απόσταση μεταξύ του οπλισμού και του πυρήνα είναι 4 εκ. Η διάμετρος εργασίας (πυρήνες με κυκλική επιφάνεια επαφής) d = 50 mm. Ο οπλισμός έλκεται μέσα στο πηνίο με δύναμη 50 kg. Το μήκος της μεσαίας γραμμής δύναμης lav = 40 εκ. Προσδιορίστε το n. σελ. και το ρεύμα του πηνίου αν υπάρχουν 3000 στροφές.

Ρύζι. 5. Ηλεκτρομαγνητική βαλβίδα φρένου DC

Η περιοχή του τμήματος εργασίας του ηλεκτρομαγνήτη είναι ίση με την περιοχή ενός κύκλου με διάμετρο d = 5 cm:

S = (π ∙ d ^ 2) / 4 = 3,14 / 4 ∙ 25 = 19,6 cm2.

Η επαγωγή B που απαιτείται για τη δημιουργία μιας δύναμης F = 50 kg βρίσκεται από την εξίσωση F = 40550 ∙ B ^ 2 ∙ S,

όπου B = √ (F / (40550 ∙ S)) = √ (50 / (40550 ∙ 0,00196)) = 0,795 T.

Μαγνητική δύναμη I ∙ ω = Hс ∙ lс + Hδ ∙ δ.

Προσδιορίζουμε την αντοχή μαγνήτισης για το χάλυβα Hc ∙ lc με απλοποιημένο τρόπο, με βάση το γεγονός ότι είναι 15% I ∙ ω:

I ∙ ω = 0,15 ∙ I ∙ ω + Hδ ∙ δ; 0,85 ∙ I ∙ ω = Hδ ∙ δ; 0,85 ∙ I ∙ ω = 8 ∙ 10 ^ 5 ∙ B ∙ δ; I ∙ ω = (8 ∙ 10 ^ 5 ∙ 0,795 ∙ 0,04) / 0,85 = 30.000 Av.

Ρεύμα μαγνήτισης I = (I ∙ ω) / ω = 30000/3000 = 10 A.