Διηλεκτρική αντοχή της μόνωσης. Παραδείγματα υπολογισμού

Με μια σταδιακή αύξηση της τάσης U μεταξύ αγωγών που χωρίζονται από ένα διηλεκτρικό (μόνωση), για παράδειγμα, πλάκες πυκνωτών ή καλώδια αγώγιμων καλωδίων, η ένταση (ισχύς) του ηλεκτρικού πεδίου στο διηλεκτρικό αυξάνεται. Η ισχύς του ηλεκτρικού πεδίου στο διηλεκτρικό αυξάνεται επίσης καθώς μειώνεται η απόσταση μεταξύ των συρμάτων.

Σε μια ορισμένη ένταση πεδίου, συμβαίνει μια βλάβη στο διηλεκτρικό, σχηματίζεται ένας σπινθήρας ή ένα τόξο και ένα ηλεκτρικό ρεύμα εμφανίζεται στο κύκλωμα. Η ένταση του ηλεκτρικού πεδίου στο οποίο συμβαίνει η διάσπαση της μόνωσης ονομάζεται ηλεκτρική αντοχή Epr της μόνωσης.

Η διηλεκτρική αντοχή ορίζεται ως η τάση ανά mm πάχους μόνωσης και μετράται σε V/mm (kV/mm) ή kV/cm. Για παράδειγμα, η διηλεκτρική ισχύς του αέρα μεταξύ λείων πλακών είναι 32 kV / cm.

Η ισχύς του ηλεκτρικού πεδίου σε ένα διηλεκτρικό για την περίπτωση που οι αγωγοί έχουν τη μορφή πλακών ή λωρίδων που χωρίζονται με ίσο διάκενο (για παράδειγμα, σε πυκνωτή χαρτιού) υπολογίζεται από τον τύπο

E = U / d,

όπου U είναι η τάση μεταξύ των καλωδίων, V (kV); d — πάχος του διηλεκτρικού στρώματος, mm (cm).

Παραδείγματα του

1. Ποια είναι η ένταση του ηλεκτρικού πεδίου στο διάκενο αέρα πάχους 3 cm μεταξύ των πλακών εάν η τάση μεταξύ τους είναι U = 100 kV (Εικ. 1);

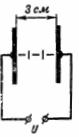
Ρύζι. 1.

Η ένταση του ηλεκτρικού πεδίου είναι: E = U / d = 100000/3 = 33333 V / cm.

Μια τέτοια τάση υπερβαίνει τη διηλεκτρική ισχύ του αέρα (32 kV / cm) και υπάρχει κίνδυνος καταστροφής.

Ο κίνδυνος ζημιάς DC μπορεί να αποφευχθεί αυξάνοντας το διάκενο, για παράδειγμα, στα 5 cm, ή χρησιμοποιώντας άλλη, ισχυρότερη μόνωση αντί για αέρα, όπως ηλεκτρικό χαρτόνι (Εικ. 2).

Ρύζι. 2.

Το ηλεκτρικό χαρτόνι έχει διηλεκτρική σταθερά ε = 2 και διηλεκτρική ισχύ 80.000 V/cm. Στην περίπτωσή μας, η ένταση ηλεκτρικού πεδίου στη μόνωση είναι 33333 V. Ο αέρας δεν μπορεί να αντέξει αυτή τη δύναμη, ενώ το ηλεκτρικό χαρτόνι σε αυτή την περίπτωση έχει απόθεμα διηλεκτρικής ισχύος 80.000/33333 = 2,4, αφού η διηλεκτρική αντοχή του ηλεκτρικού κουτιού είναι 80.000/32.000 = 2,5 φορές από αυτόν του αέρα.

2. Ποια είναι η ένταση του ηλεκτρικού πεδίου στο διηλεκτρικό ενός πυκνωτή πάχους 3 mm εάν ο πυκνωτής είναι συνδεδεμένος σε τάση U = 6 kV;

E = U / d = 6000 / 0,3 = 20000 V / cm.

3. Ένα διηλεκτρικό με πάχος 2 mm διασπάται σε τάση 30 kV. Ποια ήταν η ηλεκτρική του αντοχή;

E = U / d = 30.000 / 0,2 = 150.000 V / cm = 150 kV / cm. Το γυαλί έχει τέτοια ηλεκτρική αντοχή.

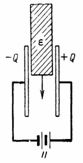
4. Ο χώρος μεταξύ των πλακών του πυκνωτή γεμίζει με στρώματα ηλεκτρικού χαρτονιού και ένα στρώμα μαρμαρυγίας ίδιου πάχους (Εικ. 3). Η τάση μεταξύ των πλακών του πυκνωτή είναι U = 10000 V. Το ηλεκτρικό χαρτόνι έχει διηλεκτρική σταθερά ε1 = 2 και μαρμαρυγία ε2 = 8.Πώς θα κατανεμηθεί η τάση U μεταξύ των στρώσεων μόνωσης και τι ένταση θα έχει το ηλεκτρικό πεδίο στα επιμέρους στρώματα;

Ρύζι. 3.

Οι τάσεις U1 και U2 στα διηλεκτρικά στρώματα του ίδιου πάχους δεν θα είναι ίσες. Η τάση του πυκνωτή θα χωριστεί σε τάσεις U1 και U2, οι οποίες θα είναι αντιστρόφως ανάλογες με τις διηλεκτρικές σταθερές:

U1 / U2 = ε2 / ε1 = 8/2 = 4/1 = 4;

U1 = 4 ∙ U2.

Αφού U = U1 + U2, έχουμε δύο εξισώσεις με δύο αγνώστους.

Αντικαταστήστε την πρώτη εξίσωση με τη δεύτερη: U = 4 ∙ U2 + U2 = 5 ∙ U2.

Επομένως, 10000 V = 5 ∙ U2; U2 = 2000 V; U1 = 4, U2 = 8000V.

Αν και τα διηλεκτρικά στρώματα έχουν το ίδιο πάχος, δεν είναι εξίσου φορτισμένα. Ένα διηλεκτρικό με υψηλότερη διηλεκτρική σταθερά είναι λιγότερο φορτισμένο (U2 = 2000 V) και αντίστροφα (U1 = 8000 V).

Η ένταση ηλεκτρικού πεδίου Ε στα διηλεκτρικά στρώματα είναι ίση με:

E1 = U1 / d1 = 8000 / 0,2 = 40.000 V / cm;

E2 = U2 / d2 = 2000 / 0,2 = 10000 V / cm.

Η διαφορά στη διηλεκτρική σταθερά οδηγεί σε αύξηση της έντασης του ηλεκτρικού πεδίου. Εάν ολόκληρο το κενό ήταν γεμάτο με ένα μόνο διηλεκτρικό, για παράδειγμα, μαρμαρυγία ή ηλεκτρικό χαρτόνι, η ένταση του ηλεκτρικού πεδίου θα ήταν μικρότερη, καθώς θα κατανεμήθηκε αρκετά ομοιόμορφα στο κενό:

E = U / d = (U1 + U2) / (d1 + d2) = 10000 / 0,4 = 25000 V / cm.

Είναι επομένως απαραίτητο να αποφευχθεί η χρήση πολύπλοκης μόνωσης με πολύ διαφορετικές διηλεκτρικές σταθερές. Για τον ίδιο λόγο, ο κίνδυνος αστοχίας αυξάνεται όταν σχηματίζονται φυσαλίδες αέρα στη μόνωση.

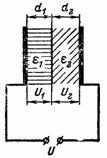
5. Προσδιορίστε την ένταση του ηλεκτρικού πεδίου στο διηλεκτρικό πυκνωτή από το προηγούμενο παράδειγμα εάν το πάχος των διηλεκτρικών στρωμάτων δεν είναι το ίδιο.Η ηλεκτρική πλακέτα έχει πάχος d1 = 0,2 mm και μαρμαρυγία d2 = 3,8 mm (Εικ. 4).

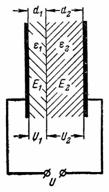
Ρύζι. 4.

Η ένταση του ηλεκτρικού πεδίου θα κατανεμηθεί αντιστρόφως ανάλογη με τις διηλεκτρικές σταθερές:

E1 / E2 = ε2 / ε1 = 8/2 = 4.

Εφόσον E1 = U1 / d1 = U1 / 0,2 και E2 = U2 / d2 = U2 / 3,8, τότε E1 / E2 = (U1 / 0,2) / (U2 / 3,8) = (U1 ∙ 3,8) / (0,2 ∙ U2) = 19 ∙ U1 / U2.

Επομένως E1 / E2 = 4 = 19 ∙ U1 / U2, ή U1 / U2 = 4/19.

Το άθροισμα των τάσεων U1 και U2 στα διηλεκτρικά στρώματα είναι ίσο με την τάση πηγής U: U = U1 + U2; 10000 = U1 + U2.

Αφού U1 = 4/19 ∙ U2, τότε 10000 = 4/10 ∙ U2 + U2 = 23/19 ∙ U2; U2 = 190.000 /23 = 8260 V; U1 = U-U2 = 1740V.

Η ισχύς του ηλεκτρικού πεδίου στη μαρμαρυγία είναι E2 ∙ 8260 / 3,8≈2174 V / cm.

Η μίκα έχει ηλεκτρική ισχύ 80.000 V / mm και μπορεί να αντέξει μια τέτοια τάση.

Η ένταση του ηλεκτρικού πεδίου στο ηλεκτρικό χαρτόνι είναι E1 = 1740 / 0,2 = 8700 V / mm.

Το ηλεκτρικό χαρτόνι δεν θα αντέξει μια τέτοια τάση, καθώς η διηλεκτρική του ισχύς είναι μόνο 8000 V / mm.

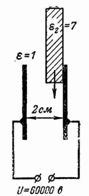
6. Μια τάση 60.000 V συνδέεται σε δύο μεταλλικές πλάκες σε απόσταση 2 εκ. Προσδιορίστε την ένταση του ηλεκτρικού πεδίου στο διάκενο αέρα, καθώς και την ένταση του ηλεκτρικού πεδίου στον αέρα και το γυαλί εάν υπάρχει γυαλί στο διάκενο εισάγει μια πλάκα με πάχος 1 cm (Εικ. 5).

Ρύζι. 5.

Εάν υπάρχει μόνο αέρας μεταξύ των πλακών, η ένταση του ηλεκτρικού πεδίου σε αυτό είναι ίση με: E = U / d = 60.000 /2 = 30.000 V / cm.

Η ένταση του πεδίου είναι κοντά στη διηλεκτρική ισχύ του αέρα.Εάν μια γυάλινη πλάκα πάχους 1 cm (διηλεκτρική σταθερά γυαλιού ε2 = 7) εισάγεται στο διάκενο, τότε E1 = U1 / d1 = U1 / 1 = U1. E2 = U2 / d2 = U2 / 1 = U2; E1 / E2 = ε2 / ε1 = 7/1 = U1 / U2;

U1 = 7 ∙ U2; U1 = 60.000-U2; 8 ∙ U2 = 60.000; U2 = 7500 V; E2 = U2 / d2 = 7500 V / cm.

Η ισχύς του ηλεκτρικού πεδίου στο γυαλί είναι E2 = 7,5 kV / cm και η ηλεκτρική του ισχύς είναι 150 kV / cm.

Σε αυτή την περίπτωση, το γυαλί έχει 20πλάσιο συντελεστή ασφαλείας.

Για το διάκενο αέρα έχουμε: U1 = 60.000-7500 = 52500 V; E1 = U1 / d1 = 52500 V / cm.

Σε αυτή την περίπτωση, η ισχύς του ηλεκτρικού πεδίου στο διάκενο αέρα είναι μεγαλύτερη από ό,τι στο πρώτο, χωρίς γυαλί. Μετά την εισαγωγή του γυαλιού, ολόκληρος ο συνδυασμός έχει μικρότερη αντοχή από τον αέρα μόνο.

Ο κίνδυνος θραύσης εμφανίζεται επίσης όταν το πάχος της γυάλινης πλάκας είναι ίσο με το διάκενο μεταξύ των αγώγιμων πλακών, δηλ. 2 cm, καθώς αναπόφευκτα θα υπάρχουν λεπτά κενά αέρα στο κενό που θα τρυπηθεί.

Η διηλεκτρική αντοχή του διακένου μεταξύ των αγωγών υψηλής τάσης πρέπει να ενισχυθεί με υλικά που έχουν χαμηλή διηλεκτρική σταθερά και υψηλή διηλεκτρική αντοχή, για παράδειγμα, ηλεκτρικό χαρτόνι με ε = 2. Αποφύγετε συνδυασμούς υλικών με υψηλή διηλεκτρική σταθερά (γυαλί , πορσελάνη) και αέρα, που πρέπει να αντικατασταθεί με λάδι.