Μπαταρίες. Παραδείγματα υπολογισμού

Οι μπαταρίες είναι ηλεκτροχημικές πηγές ρεύματος που, μετά την εκφόρτιση, μπορούν να φορτιστούν χρησιμοποιώντας ηλεκτρικό ρεύμα που αντλείται από φορτιστή. Όταν το ρεύμα φόρτισης ρέει στην μπαταρία, συμβαίνει ηλεκτρόλυση, με αποτέλεσμα να σχηματίζονται χημικές ενώσεις στην άνοδο και την κάθοδο που βρίσκονταν στα ηλεκτρόδια στην αρχική κατάσταση λειτουργίας της μπαταρίας.

Η ηλεκτρική ενέργεια, όταν φορτίζεται σε μια μπαταρία, μετατρέπεται σε μια χημική μορφή ενέργειας. Όταν εκφορτίζεται, η χημική μορφή της ενέργειας γίνεται ηλεκτρική. Χρειάζεται περισσότερη ενέργεια για τη φόρτιση μιας μπαταρίας από αυτή που μπορεί να ληφθεί με την αποφόρτισή της.

Η τάση κάθε στοιχείου μιας μπαταρίας μολύβδου-οξέος μετά τη φόρτιση 2,7 V δεν πρέπει να πέσει κάτω από 1,83 V κατά την εκφόρτιση.

Η μέση τάση μιας μπαταρίας νικελίου-σιδηρού είναι 1,1 V.

Τα ρεύματα φόρτισης και εκφόρτισης της μπαταρίας είναι περιορισμένα και ορίζονται από τον κατασκευαστή (περίπου 1 A ανά 1 dm2 της πλάκας).

Η ποσότητα ηλεκτρικής ενέργειας που μπορεί να αντληθεί από μια φορτισμένη μπαταρία ονομάζεται χωρητικότητα αμπέρ-ώρας της μπαταρίας.

Οι μπαταρίες χαρακτηρίζονται επίσης από ενεργειακή και τρέχουσα απόδοση.Η επιστροφή ενέργειας είναι ίση με την αναλογία της ενέργειας που λαμβάνεται κατά την εκφόρτιση προς την ενέργεια που δαπανάται για τη φόρτιση της μπαταρίας: ηen = Araz / Azar.

Για μια μπαταρία μολύβδου-οξέος ηen = 70% και για μια μπαταρία σιδήρου-νικελίου ηen = 50%.

Η έξοδος ρεύματος είναι ίση με την αναλογία της ποσότητας ηλεκτρικής ενέργειας που λαμβάνεται κατά την εκφόρτιση προς την ποσότητα ηλεκτρικής ενέργειας που καταναλώνεται κατά τη φόρτιση: ηt = Q φορές / Qchar.

Οι μπαταρίες μολύβδου-οξέος έχουν ηt = 90% και οι μπαταρίες σιδήρου-νικελίου ηt = 70%.

Υπολογισμός μπαταρίας

1. Γιατί η τρέχουσα επιστροφή της μπαταρίας είναι μεγαλύτερη από την επιστροφή ενέργειας;

ηen = Araz / Azar = (Up ∙ Ip ∙ tp) / (Uz ∙ Iz ∙ tz) = Up / Uz ∙ ηt.

Η επιστροφή ενέργειας ισούται με το ρεύμα επιστροφής ηt πολλαπλασιαζόμενο με το λόγο της τάσης εκφόρτισης προς την τάση φόρτισης. Δεδομένου ότι η αναλογία Uр / U3 <1, τότε ηen <ηt.

2. Μια μπαταρία μολύβδου-οξέος με τάση 4 V και χωρητικότητα 14 Ah φαίνεται στο σχ. 1. Η σύνδεση των πλακών φαίνεται στο σχ. 2. Η παράλληλη σύνδεση των πλακών αυξάνει τη χωρητικότητα της μπαταρίας. Δύο σετ πλακών συνδέονται σε σειρά για να αυξήσουν την τάση.

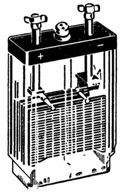
Ρύζι. 1. Μπαταρία μολύβδου-οξέος

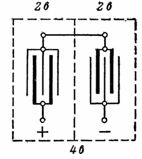
Ρύζι. 2. Σύνδεση των πλακών μιας μπαταρίας μολύβδου-οξέος για τάση 4 V

Η μπαταρία φορτίζεται σε 10 ώρες με ρεύμα Ic = 1,5 A και αποφορτίζεται σε 20 ώρες με ρεύμα Ip = 0,7 A. Ποια είναι η απόδοση ρεύματος;

Qp = Ip ∙ tp = 0,7 ∙ 20 = 14 A • h; Qz = Iz ∙ tz = 1,5 ∙ 10 = 15 A • h; ηt = Qp / Qz = 14/15 = 0,933 = 93%.

3. Η μπαταρία φορτίζεται με ρεύμα 0,7 A για 5 ώρες. Πόσο καιρό θα εκφορτίζεται με ρεύμα 0,3 A με ρεύμα εξόδου ηt = 0,9 (Εικ. 3);

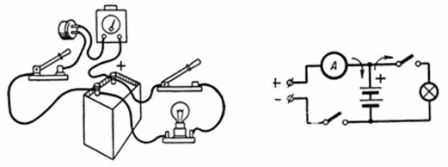
Ρύζι. 3. Σχήμα και διάγραμμα για παράδειγμα 3

Η ποσότητα ηλεκτρικής ενέργειας που χρησιμοποιείται για τη φόρτιση της μπαταρίας είναι: Qz = Iz ∙ tz = 0,7 ∙ 5 = 3,5 A • h.

Η ποσότητα ηλεκτρικής ενέργειας Qp που απελευθερώνεται κατά την εκφόρτιση υπολογίζεται με τον τύπο ηt = Qp / Qz, από όπου Qp = ηt ∙ Qz = 0,9 ∙ 3,5 = 3,15 A • h.

Χρόνος εκφόρτισης tp = Qp / Ip = 3,15 / 0,3 = 10,5 ώρες.

4. Η μπαταρία των 20 Ah φορτίστηκε πλήρως μέσα σε 10 ώρες από το δίκτυο AC μέσω ενός ανορθωτή σεληνίου (Εικ. 4). Ο θετικός ακροδέκτης του ανορθωτή συνδέεται με τον θετικό πόλο της μπαταρίας κατά τη φόρτιση. Με ποιο ρεύμα φορτίζεται η μπαταρία αν η απόδοση ρεύματος ηt = 90%; Με τι ρεύμα μπορεί να αποφορτιστεί η μπαταρία μέσα σε 20 ώρες;

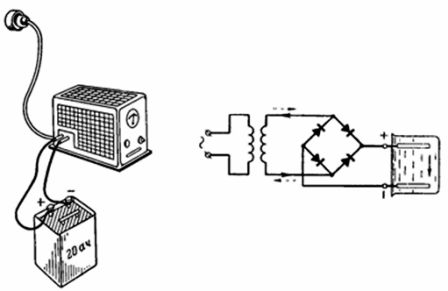
Ρύζι. 4. Σχήμα και διάγραμμα για παράδειγμα 4

Το ρεύμα φόρτισης της μπαταρίας είναι: Ic = Q / (ηt ∙ tc) = 20 / (10 ∙ 0,9) = 2,22 A. Επιτρεπόμενο ρεύμα εκφόρτισης Iр = Q / tr = 20/20 = 1 A.

5. Μια μπαταρία συσσωρευτή που αποτελείται από 50 κελιά φορτίζεται με ρεύμα 5 A. ένα στοιχείο μπαταρίας 2,1 V και η εσωτερική αντίσταση rvn = 0,005 Ohm. Ποια είναι η τάση της μπαταρίας; Τι είναι και τα λοιπά. γ) πρέπει να έχει γεννήτρια φορτίου με εσωτερική αντίσταση rg = 0,1 Ohm (Εικ. 5);

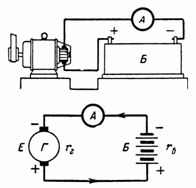
Ρύζι. 5. Σχήμα και διάγραμμα για παράδειγμα 5

Η μπαταρία D. d. C. ισούται με: Eb = 50 ∙ 2,1 = 105 V.

Εσωτερική αντίσταση της μπαταρίας rb = 50 ∙ 0,005 = 0,25 Ohm. Δ. δ. Σ. γεννήτρια ισούται με το άθροισμα του e. και τα λοιπά. με μπαταρίες και πτώση τάσης σε μπαταρία και γεννήτρια: E = U + I ∙ rb + I ∙ rg = 105 + 5 ∙ 0,25 + 5 ∙ 0,1 = 106,65 V.

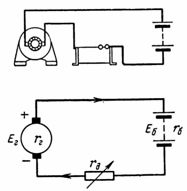
6. Η μπαταρία αποθήκευσης αποτελείται από 40 κύτταρα με εσωτερική αντίσταση rvn = 0,005 Ohm και e. και τα λοιπά. σελ. 2,1 V. Η μπαταρία φορτίζεται με ρεύμα I = 5 A από τη γεννήτρια, π.χ. και τα λοιπά. μεπου είναι 120 V και η εσωτερική αντίσταση rg = 0,12 Ohm. Προσδιορίστε την πρόσθετη αντίσταση rd, την ισχύ της γεννήτριας, τη χρήσιμη ισχύ της φόρτισης, την απώλεια ισχύος στην πρόσθετη αντίσταση rd και την απώλεια ισχύος στην μπαταρία (Εικ. 6).

Ρύζι. 6. Υπολογισμός του συσσωρευτή

Βρείτε πρόσθετη αντίσταση χρησιμοποιώντας Ο δεύτερος νόμος του Kirchhoff:

Eg = Eb + rd ∙ I + rg ∙ I + 40 ∙ rv ∙ I; rd = (Π.χ.-Eb-I ∙ (rg + 40 ∙ rv)) / I = (120-84-5 ∙ (0,12 + 0,2)) / 5 = 34,4 / 5 = 6,88 Ohm…

Αφού ε. κ.λπ. γ. Όταν φορτιστεί η μπαταρία, το EMF της κυψέλης στην αρχή της φόρτισης είναι 1,83 V, στη συνέχεια στην αρχή της φόρτισης, με σταθερή πρόσθετη αντίσταση, το ρεύμα θα είναι μεγαλύτερο από 5 Α. Για να διατηρηθεί σταθερή φόρτιση ρεύμα, είναι απαραίτητο να αλλάξετε την πρόσθετη αντίσταση.

Απώλεια ισχύος στην πρόσθετη αντίσταση ∆Pd = rd ∙ I ^ 2 = 6,88 ∙ 5 ^ 2 = 6,88 ∙ 25 = 172 W.

Απώλεια ισχύος στη γεννήτρια ∆Pg = rg ∙ I ^ 2 = 0,12 ∙ 25 = 3 W.

Απώλεια ισχύος στην εσωτερική αντίσταση της μπαταρίας ∆Pb = 40 ∙ rvn ∙ I ^ 2 = 40 ∙ 0,005 ∙ 25 = 5 W.

Η παρεχόμενη ισχύς της γεννήτριας στο εξωτερικό κύκλωμα είναι Pg = Eb ∙ I + Pd + Pb = 84 ∙ 5 + 172 + 5 = 579 W.

Χρήσιμη ισχύς φόρτισης Ps = Eb ∙ I = 420 W.