Υπολογισμός χωρητικότητας πυκνωτή

Η χωρητικότητα C είναι η ικανότητα του πυκνωτή να δέχεται (αποθηκεύει και συγκρατεί) την ποσότητα ηλεκτρικής ενέργειας Q σε αμπέρ-δευτερόλεπτα ή τη φόρτιση Q σε μενταγιόν. Εάν πείτε σε ένα σώμα, για παράδειγμα σε μια μπάλα, ένα ηλεκτρικό φορτίο (ποσότητα ηλεκτρικής ενέργειας) Q, τότε ένα ηλεκτροσκόπιο που συνδέεται μεταξύ αυτού του σώματος και της γείωσης θα δείξει τάση U (Εικ. 1). Αυτή η τάση είναι ανάλογη του φορτίου και εξαρτάται επίσης από το σχήμα και το μέγεθος του σώματος.

Η σχέση μεταξύ φορτίου Q και τάσης U εκφράζεται με τον τύπο Q = C ∙ U.

Η σταθερά της αναλογικότητας C ονομάζεται χωρητικότητα του σώματος. Αν το σώμα έχει σχήμα μπάλας, η χωρητικότητα του σώματος είναι ανάλογη με την ακτίνα της μπάλας r.

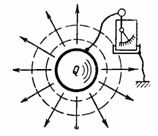
Ρύζι. 1.

Η μονάδα μέτρησης της χωρητικότητας είναι το farad (F).

Το σώμα έχει χωρητικότητα 1 F όταν ένα φορτίο 1 k παράγει τάση 1 V. μεταξύ αυτού και του εδάφους. Τα Farads είναι μια πολύ μεγάλη μονάδα μέτρησης, επομένως χρησιμοποιούνται μικρότερες μονάδες στην πράξη: microfarad (μF), nanofarad (nF) και picofarad (pF)...

Αυτές οι μονάδες σχετίζονται με τους ακόλουθους λόγους: 1 Ф = 10 ^ 6 μF; 1 μF = 10 ^ 6 pF; 1 nF = 10 ^ 3 pF.

Η χωρητικότητα μιας μπάλας με ακτίνα 1 cm είναι 1,1 pF.

Όχι μόνο ένα απομονωμένο σώμα μπορεί να συσσωρεύσει φορτίο, αλλά και μια ειδική συσκευή που ονομάζεται πυκνωτής. Ένας πυκνωτής αποτελείται από δύο ή περισσότερες πλάκες (πλάκες) που χωρίζονται από ένα διηλεκτρικό (μόνωση).

Στο σχ. Το σχήμα 2 δείχνει ένα κύκλωμα με μια πηγή DC συνδεδεμένη σε έναν πυκνωτή. Όταν είναι ενεργοποιημένο, σχηματίζεται ένα θετικό φορτίο +Q στη δεξιά πλάκα του πυκνωτή και ένα αρνητικό φορτίο –Q στην αριστερή πλάκα. Στη διάρκεια φορτίο πυκνωτή ένα ρεύμα ρέει μέσω του κυκλώματος, το οποίο σταματά μετά το τέλος της φόρτισης. τότε η τάση στον πυκνωτή θα είναι ίση με e. και τα λοιπά. γ. πηγή U. Το φορτίο στην πλάκα του πυκνωτή, η τάση και η χωρητικότητα σχετίζονται με την αναλογία Q = C ∙ U. Σε αυτήν την περίπτωση, σχηματίζεται ένα ηλεκτροστατικό πεδίο στο διηλεκτρικό του πυκνωτή.

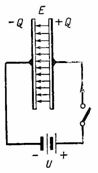
Ρύζι. 2.

Η χωρητικότητα ενός πυκνωτή με διηλεκτρικό αέρα μπορεί να υπολογιστεί με τον τύπο C = S / (4 ∙ π ∙ d) ∙ 1,11, pF, όπου S είναι το εμβαδόν μιας πλάκας, cm2. d είναι η απόσταση μεταξύ των πλακών, cm. C είναι η χωρητικότητα του πυκνωτή, pF.

Η χωρητικότητα ενός πυκνωτή που αποτελείται από n πλάκες (Εικ. 3) είναι ίση με: C = (n-1) ∙ S / (4 ∙ π ∙ δ) ∙ 1,11, pF.

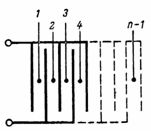
Ρύζι. 3.

Εάν ο χώρος μεταξύ των πλακών γεμίσει με άλλο διηλεκτρικό, για παράδειγμα χαρτί, η χωρητικότητα του πυκνωτή θα αυξηθεί κατά ένα συντελεστή ε. Όταν χρησιμοποιείται μόνωση χαρτιού, η χωρητικότητα θα αυξηθεί 3 φορές, με μόνωση μαρμαρυγίας — 5-8 φορές, με γυαλί — 7 φορές κ.λπ. Η τιμή του ε ονομάζεται διηλεκτρική σταθερά του διηλεκτρικού.

Ο γενικός τύπος για τον προσδιορισμό της χωρητικότητας ενός πυκνωτή με διηλεκτρική σταθερά ε (έψιλον) είναι: C = ε ∙ S / (4 ∙ π ∙ δ) ∙ 1,11, pF.

Αυτός ο τύπος είναι χρήσιμος για τον υπολογισμό μικρών μεταβλητών πυκνωτών για ραδιόφωνα.Ο ίδιος τύπος μπορεί να αναπαρασταθεί ως: C = (ε_0 ∙ ε ∙ S) / d, όπου ε_0 είναι η διηλεκτρική σταθερά ή η διηλεκτρική σταθερά του κενού (ε_0 = 8,859 ∙ 10 ^ (- 12) F / m); ε είναι η διηλεκτρική σταθερά του διηλεκτρικού.

Σε αυτόν τον τύπο, οι διαστάσεις αντικαθίστανται σε μέτρα και η χωρητικότητα λαμβάνεται σε farads.

Παραδείγματα του

1. Ποια είναι η χωρητικότητα του πλανήτη Γη, του οποίου η ακτίνα είναι r = 6378 km;

Δεδομένου ότι η χωρητικότητα μιας σφαίρας με ακτίνα 1 cm είναι ίση με 1,11 pF, η χωρητικότητα της Γης είναι: C = 637,8 ∙ 10 ^ 6 ∙ 1,11 = 707,95 ∙ 10 ^ 6 pF = 708 μF. (Η χωρητικότητα μιας μπάλας στο μέγεθος του πλανήτη μας είναι σχετικά μικρή. Οι μικρού μεγέθους ηλεκτρολυτικοί πυκνωτές έχουν αυτήν την ικανότητα).

2. Προσδιορίστε τη χωρητικότητα ενός πυκνωτή που αποτελείται από δύο πλάκες, καθεμία από τις οποίες έχει εμβαδόν S = 120 cm2.

Οι πλάκες χωρίζονται από ένα στρώμα αέρα με πάχος d = 0,5 cm, C = S / (4 ∙ π ∙ d) ∙ 1,11 = (120 ∙ 1,11) / (4 ∙ π ∙ 0,5) = 21 ,20 pF ...

3. Προσδιορίστε την χωρητικότητα του πυκνωτή με τα δεδομένα που δίνονται στο προηγούμενο παράδειγμα, εάν ο χώρος μεταξύ των πλακών είναι γεμάτος με χαρτί κεριού με διηλεκτρική σταθερά ε = 4, γυαλί (ε = 7), ηλεκτρικό χαρτόνι (ε = 2) , μαρμαρυγία (ε = 8 ).

Ένας πυκνωτής χαρτιού κεριού έχει χωρητικότητα C = ε ∙ (S ∙ 1,11) / (4 ∙ π ∙ d) = 4 ∙ 21,2 = 84,8 pF.

Η χωρητικότητα ενός γυάλινου πυκνωτή είναι C = 7 ∙ 21,2 = 148,4 pF.

Η χωρητικότητα του πυκνωτή από χαρτόνι είναι C = 2 ∙ 21,2 = 42,3 pF.

Η χωρητικότητα του πυκνωτή μαρμαρυγίας είναι C = 8 ∙ 21,2 = 169,6 pF.

4. Ποια είναι η χωρητικότητα ενός περιστροφικού πυκνωτή αέρα για έναν ραδιοφωνικό δέκτη που αποτελείται από 20 πλάκες με εμβαδόν 20 cm2 εάν η απόσταση μεταξύ των πλακών είναι 0,06 cm (Εικ. 149);

C = (n-1) ∙ (S ∙ 1,11) / (4 ∙ π ∙ δ) = (20-1) ∙ (20 ∙ 1,11) / (4 ∙ π ∙ 0,06) = 559, 44 pF.

Ο πυκνωτής που φαίνεται στο Σχ.3, αποτελείται από ξεχωριστούς απλούστερους πυκνωτές με δύο πλάκες, ο αριθμός των οποίων είναι ίσος με n-1.

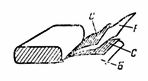
5. Ένας χάρτινος πυκνωτής χωρητικότητας C = 2 μF αποτελείται από δύο λωρίδες αλουμινόχαρτου C και δύο λωρίδες διηλεκτρικού από κέρινο χαρτί Β με διηλεκτρική σταθερά ε = 6. Το πάχος του κεριού χαρτιού είναι d = 0,1 mm. Οι διπλωμένες λωρίδες τυλίγονται, οι αγωγοί είναι κατασκευασμένοι από χαλύβδινες πλάκες. Προσδιορίστε το μήκος της χαλύβδινης λωρίδας συμπυκνωτή εάν το πλάτος της είναι 4 cm (Εικ. 4).

Ρύζι. 4.

Αρχικά, προσδιορίζουμε το εμβαδόν μιας λωρίδας με τον τύπο C = ε ∙ S / (4 ∙ π ∙ δ) ∙ 1,11, από όπου S = (C ∙ 4 ∙ π ∙ d) / (ε ∙ 1,11) = ( 2 ∙ 4 ∙ π ∙ 0,01 ∙ 10 ^ 6) / (6 ∙ 1,11); S = 2.000.000 / (6 ∙ 1,11) ∙ 4 ∙ π ∙ 0,01 = 37680 cm2.

Το μήκος κάθε λωρίδας είναι l = 37680/4 = 9420 cm = 94,2 m.