Μη γραμμικά ηλεκτρικά κυκλώματα
Σκοπός μη γραμμικών στοιχείων σε ηλεκτρικά κυκλώματα
V ηλεκτρικά κυκλώματα μπορεί να περιλαμβάνει παθητικά στοιχεία, ηλεκτρική αντίσταση που ουσιαστικά εξαρτάται από το ρεύμα ή την τάση, με αποτέλεσμα το ρεύμα να μην είναι ευθέως ανάλογο της τάσης. Τέτοια στοιχεία και τα ηλεκτρικά κυκλώματα στα οποία εισέρχονται ονομάζονται μη γραμμικά στοιχεία.
Τα μη γραμμικά στοιχεία δίνουν στα ηλεκτρικά κυκλώματα ιδιότητες ανέφικτες σε γραμμικά κυκλώματα (σταθεροποίηση τάσης ή ρεύματος, ενίσχυση DC, κ.λπ.). Είναι ανεξέλεγκτες και ελεγχόμενες... Το πρώτο — διπολικό — έχει σχεδιαστεί για να λειτουργεί χωρίς την επίδραση ενός παράγοντα ελέγχου πάνω τους (θερμίστορ ημιαγωγών και δίοδοι), και το δεύτερο — πολυπολικό — χρησιμοποιείται όταν ένας παράγοντας ελέγχου ενεργεί πάνω τους (τρανζίστορ και θυρίστορ).
Χαρακτηριστικά ρεύματος-τάσης μη γραμμικών στοιχείων
Οι ηλεκτρικές ιδιότητες των μη γραμμικών στοιχείων είναι χαρακτηριστικά ρεύματος-τάσης I (U) πειραματικά γραφήματα που δείχνουν την εξάρτηση του ρεύματος από την τάση, για τα οποία μερικές φορές γίνεται ένας κατά προσέγγιση, βολικός για υπολογισμό εμπειρικός τύπος.
Τα μη ελεγχόμενα μη γραμμικά στοιχεία έχουν ένα μοναδικό χαρακτηριστικό ρεύματος-τάσης και τα ελεγχόμενα μη γραμμικά στοιχεία έχουν μια οικογένεια τέτοιων χαρακτηριστικών των οποίων η παράμετρος είναι ο συντελεστής ελέγχου.
Τα γραμμικά στοιχεία έχουν σταθερή ηλεκτρική αντίσταση, επομένως το χαρακτηριστικό ρεύματος-τάσης τους είναι μια ευθεία γραμμή που διέρχεται από την αρχή (Εικ. 1, α).
Τα χαρακτηριστικά ρεύματος-τάσης των μη γραμμικών έχουν διαφορετικό σχήμα και χωρίζονται σε συμμετρικά και ασύμμετρα ως προς τους άξονες συντεταγμένων (Εικ. 1, β, γ).
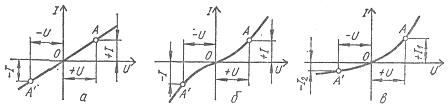
Ρύζι. 1. Χαρακτηριστικά ρεύματος-τάσης παθητικών στοιχείων: α — γραμμικό, β — μη γραμμικό συμμετρικό, γ — μη γραμμικό ασύμμετρο
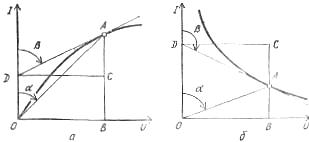
Ρύζι. 2. Γραφήματα για τον προσδιορισμό της στατικής προς διαφορική αντίσταση των μη γραμμικών στοιχείων στα τμήματα των χαρακτηριστικών ρεύματος-τάσης: α — ανοδική, β — πτώση
Για μη γραμμικά στοιχεία με συμμετρικό χαρακτηριστικό ρεύματος-τάσης ή για συμμετρικά στοιχεία, μια αλλαγή στην κατεύθυνση της τάσης δεν προκαλεί αλλαγή στην τιμή ρεύματος (Εικ. 1, β) και για μη γραμμικά στοιχεία με ασύμμετρη τάση -χαρακτηριστικό ρεύματος, ή για ασύμμετρα στοιχεία, με μία και την ίδια απόλυτη τιμή της τάσης που κατευθύνεται σε αντίθετες κατευθύνσεις, τα ρεύματα είναι διαφορετικά (Εικ. 1, γ). Επομένως, μη γραμμικά συμμετρικά στοιχεία χρησιμοποιούνται σε κυκλώματα συνεχούς ρεύματος και εναλλασσόμενου ρεύματος και μη γραμμικά μη ισορροπημένα στοιχεία, κατά κανόνα, σε κυκλώματα εναλλασσόμενου ρεύματος για τη μετατροπή AC σε ρεύμα συνεχούς ρεύματος.
Χαρακτηριστικά μη γραμμικών στοιχείων
Για κάθε μη γραμμικό στοιχείο, διακρίνεται μια στατική αντίσταση που αντιστοιχεί σε ένα δεδομένο σημείο του χαρακτηριστικού ρεύματος-τάσης, για παράδειγμα το σημείο Α:
Rst = U / I = muOB / miBA = mr tgα
και η διαφορική αντίσταση που είναι για. το ίδιο σημείο Α προσδιορίζεται από τον τύπο:
Rdiff = dU / dI = muDC / miCA = mr tgβ,
όπου mi, mi, κύριε — αντίστοιχα η κλίμακα των τάσεων, των ρευμάτων και των αντιστάσεων.
Η στατική αντίσταση χαρακτηρίζει τις ιδιότητες ενός μη γραμμικού στοιχείου στη λειτουργία σταθερού ρεύματος και τη διαφορική αντίσταση — για μικρές αποκλίσεις του ρεύματος από την τιμή σταθερής κατάστασης. Και τα δύο αλλάζουν όταν περνούν από ένα σημείο και το χαρακτηριστικό ρεύματος-τάσης σε άλλο, το πρώτο είναι πάντα θετικό και το δεύτερο μεταβλητό: στο ανοδικό τμήμα του χαρακτηριστικού, το ρεύμα-τάση είναι θετικό και στο τμήμα πτώσης είναι αρνητικό.
Τα μη γραμμικά στοιχεία χαρακτηρίζονται επίσης από αμοιβαίες τιμές: στατική αγωγιμότητα Gst και διαφορική αγωγιμότητα GΔιαφορετικές ή αδιάστατες παράμετροι —
σχετική αντίσταση:
Kr = — (Rdifference /Rst)
ή σχετική αγωγιμότητα:
Kg = — (Gdifference / Gst)
Τα γραμμικά στοιχεία έχουν παραμέτρους Kr και Kilogram ίσες με ένα και για τα μη γραμμικά στοιχεία διαφέρουν από αυτό και όσο περισσότερο διαφέρουν από ένα, τόσο περισσότερο εκδηλώνεται η μη γραμμικότητα του ηλεκτρικού κυκλώματος.
 Υπολογισμός μη γραμμικών ηλεκτρικών κυκλωμάτων
Υπολογισμός μη γραμμικών ηλεκτρικών κυκλωμάτων
Τα μη γραμμικά ηλεκτρικά κυκλώματα υπολογίζονται γραφικά και αναλυτικά με βάση Οι νόμοι του Kirchhoff και χαρακτηριστικά βολτ-αμπέρ επιμέρους στοιχείων κυκλωμάτων εναλλασσόμενου ρεύματος για μετατροπή εναλλασσόμενου ρεύματος σε συνεχές ρεύμα.
Όταν υπολογίζετε γραφικά ένα ηλεκτρικό κύκλωμα με δύο συνδεδεμένες σε σειρά μη γραμμικές αντιστάσεις R1 και R2 με χαρακτηριστικά τάσης ρεύματος Iz (U1) και Iz (U2), να δημιουργήσετε το χαρακτηριστικό ρεύματος-τάσης ολόκληρου του κυκλώματος Iz (U), όπου U = U1 + U2, οι τετμήσεις των σημείων των οποίων βρίσκονται αθροίζοντας τις τετμημένες των σημείων των χαρακτηριστικών ρεύματος-τάσης μη γραμμικών αντιστάσεων με ίσες τεταγμένες (Εικ. 3, α, β).
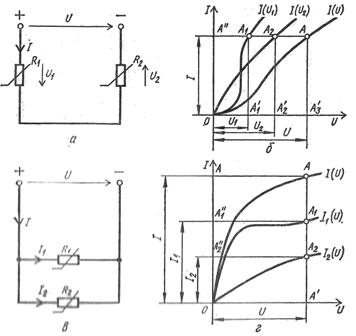
Ρύζι. 3. Διαγράμματα και χαρακτηριστικά μη γραμμικών ηλεκτρικών κυκλωμάτων: α — κύκλωμα σειριακής σύνδεσης μη γραμμικών αντιστάσεων, β — χαρακτηριστικά βολτ-αμπέρ επιμέρους στοιχείων και κυκλώματος σειράς, γ — σχήμα παράλληλης σύνδεσης μη γραμμικών αντιστάσεων, d — χαρακτηριστικά βολτ-αμπέρ μεμονωμένων στοιχείων και παράλληλου κυκλώματος.
Η παρουσία αυτής της καμπύλης επιτρέπει στην τάση U να βρει το ρεύμα Az καθώς και την τάση U1 και U2 στους ακροδέκτες των αντιστάσεων.
Με τον ίδιο τρόπο πραγματοποιείται ο υπολογισμός του ηλεκτρικού κυκλώματος με δύο αντιστάσεις συνδεδεμένες παράλληλα. R1 και R2 με χαρακτηριστικά ρεύματος-τάσης I1 (U) και Az2 (U), για τα οποία κατασκευάστηκε το χαρακτηριστικό ρεύματος-τάσης ολόκληρου του κυκλώματος Az(U), όπου Az = I1+I2, στο οποίο, χρησιμοποιώντας μια δεδομένη τάση U, βρείτε τα ρεύματα Az , I1, I2 (oriz. 3, c, d).
Η αναλυτική μέθοδος για τον υπολογισμό των μη γραμμικών ηλεκτρικών κυκλωμάτων βασίζεται στην παρουσίαση των χαρακτηριστικών τάσης των μη γραμμικών στοιχείων μέσω των εξισώσεων των αντίστοιχων μαθηματικών συναρτήσεων, οι οποίες καθιστούν δυνατή τη σύνταξη των απαραίτητων εξισώσεων κατάστασης για τα ηλεκτρικά κυκλώματα. .Δεδομένου ότι η λύση τέτοιων μη γραμμικών εξισώσεων συχνά προκαλεί σημαντικές δυσκολίες, η αναλυτική μέθοδος για τον υπολογισμό των μη γραμμικών κυκλωμάτων είναι βολική όταν τα λειτουργικά τμήματα των χαρακτηριστικών ρεύματος-τάσης των μη γραμμικών στοιχείων μπορούν να ευθυγραμμιστούν. Αυτό σας επιτρέπει να περιγράψετε την ηλεκτρική κατάσταση του κυκλώματος με γραμμικές εξισώσεις που δεν δημιουργούν δυσκολίες στην επίλυσή τους.
Βασικές αρχές Ηλεκτρολόγων Μηχανικών:
Στη διαφορά δυναμικού, την ηλεκτροκινητική δύναμη και την τάση
Ηλεκτρικό ρεύμα σε υγρά και αέρια
Μαγνητισμός και Ηλεκτρομαγνητισμός
Σχετικά με το μαγνητικό πεδίο, τις ηλεκτρομαγνήτες και τους ηλεκτρομαγνήτες
Αυτοεπαγωγή και αμοιβαία επαγωγή
Ηλεκτρικό πεδίο, ηλεκτροστατική επαγωγή, χωρητικότητα και πυκνωτές
Τι είναι το εναλλασσόμενο ρεύμα και σε τι διαφέρει από το συνεχές ρεύμα

