Τι είναι το εναλλασσόμενο ρεύμα και σε τι διαφέρει από το συνεχές ρεύμα

Εναλλασσόμενο ρεύμα, Αντίθετα Ρεύμα συνεχούς ρεύματος, αλλάζει συνεχώς τόσο σε μέγεθος όσο και σε κατεύθυνση, και αυτές οι αλλαγές συμβαίνουν περιοδικά, δηλαδή επαναλαμβάνονται σε ακριβώς ίσα διαστήματα.

Για να προκληθεί ένα τέτοιο ρεύμα στο κύκλωμα, χρησιμοποιήστε πηγές εναλλασσόμενου ρεύματος που δημιουργούν ένα εναλλασσόμενο EMF, που αλλάζει περιοδικά σε μέγεθος και κατεύθυνση.Τέτοιες πηγές ονομάζονται εναλλάκτες.

Στο σχ. Το 1 δείχνει ένα διάγραμμα συσκευής (μοντέλο) από τα πιο απλά εναλλάκτης. 

Ένα ορθογώνιο πλαίσιο από χάλκινο σύρμα, στερεωμένο στον άξονα και περιστρεφόμενο στο χωράφι χρησιμοποιώντας ιμάντα κίνησης μαγνήτης… Τα άκρα του πλαισίου συγκολλούνται σε χάλκινους δακτυλίους, οι οποίοι, περιστρέφοντας με το πλαίσιο, γλιστρούν στις πλάκες επαφής (βούρτσες).

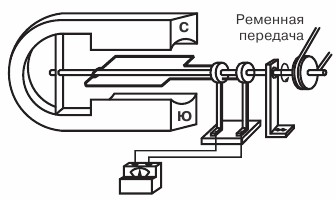
Εικόνα 1. Διάγραμμα του απλούστερου εναλλάκτη

Ας βεβαιωθούμε ότι μια τέτοια συσκευή είναι πραγματικά πηγή μεταβλητού EMF.

Ας υποθέσουμε ότι ένας μαγνήτης δημιουργεί ανάμεσα στους πόλους του ομοιόμορφο μαγνητικό πεδίο, δηλαδή ένα στο οποίο η πυκνότητα των γραμμών μαγνητικού πεδίου σε κάθε τμήμα του πεδίου είναι ίδια.περιστρέφοντας, το πλαίσιο διασχίζει τις γραμμές δύναμης του μαγνητικού πεδίου σε κάθε πλευρά του a και b EMF που προκαλείται. 

Οι πλευρές c και d του πλαισίου δεν λειτουργούν, γιατί όταν το πλαίσιο περιστρέφεται, δεν διασχίζουν τις γραμμές δύναμης του μαγνητικού πεδίου και επομένως δεν συμμετέχουν στη δημιουργία του EMF.

Ανά πάσα στιγμή, το EMF που εμφανίζεται στην πλευρά α είναι αντίθετη ως προς την κατεύθυνση του EMF που εμφανίζεται στην πλευρά b, αλλά στο πλαίσιο και τα δύο EMF ενεργούν σύμφωνα και προστίθενται στο συνολικό EMF, δηλαδή επάγεται από ολόκληρο το πλαίσιο.

Αυτό είναι εύκολο να ελεγχθεί εάν χρησιμοποιούμε τον κανόνα του δεξιού χεριού που γνωρίζουμε για να καθορίσουμε την κατεύθυνση του EMF.

Για να το κάνετε αυτό, τοποθετήστε την παλάμη του δεξιού χεριού έτσι ώστε να βλέπει προς τον βόρειο πόλο του μαγνήτη και ο λυγισμένος αντίχειρας συμπίπτει με την κατεύθυνση κίνησης εκείνης της πλευράς του πλαισίου στην οποία θέλουμε να προσδιορίσουμε την κατεύθυνση του EMF. Στη συνέχεια, η κατεύθυνση του EMF σε αυτό θα υποδεικνύεται από τα τεντωμένα δάχτυλα του χεριού.

Για όποια θέση του πλαισίου προσδιορίζουμε την κατεύθυνση του EMF στις πλευρές a και b, πάντα αθροίζονται και σχηματίζουν ένα συνολικό EMF στο πλαίσιο. Ταυτόχρονα, με κάθε περιστροφή του πλαισίου, η κατεύθυνση του συνολικού EMF σε αυτό αλλάζει προς το αντίθετο, αφού κάθε μία από τις πλευρές εργασίας του πλαισίου σε μία περιστροφή περνά κάτω από διαφορετικούς πόλους του μαγνήτη.

Το μέγεθος του EMF που προκαλείται στο πλαίσιο αλλάζει επίσης καθώς αλλάζει ο ρυθμός με τον οποίο οι πλευρές του πλαισίου διασχίζουν τις γραμμές του μαγνητικού πεδίου. Πράγματι, τη στιγμή που το πλαίσιο πλησιάζει την κατακόρυφη θέση του και το περνά, η ταχύτητα διέλευσης των γραμμών δύναμης στις πλευρές του πλαισίου είναι η υψηλότερη και το μεγαλύτερο emf προκαλείται στο πλαίσιο.Εκείνες τις χρονικές στιγμές, όταν το πλαίσιο περνάει την οριζόντια θέση του, οι πλευρές του φαίνονται να γλιστρούν κατά μήκος των γραμμών του μαγνητικού πεδίου χωρίς να τις διασχίζουν και δεν προκαλείται EMF.

Επομένως, με ομοιόμορφη περιστροφή του πλαισίου, θα προκληθεί ένα EMF σε αυτό, αλλάζοντας περιοδικά τόσο σε μέγεθος όσο και σε κατεύθυνση.

Το EMF που εμφανίζεται στο πλαίσιο μπορεί να μετρηθεί από μια συσκευή και να χρησιμοποιηθεί για τη δημιουργία ρεύματος στο εξωτερικό κύκλωμα.

Χρησιμοποιώντας φαινόμενο ηλεκτρομαγνητικής επαγωγής, μπορείτε να λάβετε εναλλασσόμενο EMF και επομένως εναλλασσόμενο ρεύμα.

Εναλλασσόμενο ρεύμα για βιομηχανικούς σκοπούς και για φωτισμό παράγονται από ισχυρές γεννήτριες που κινούνται από ατμοστρόβιλους ή υδροστρόβιλους και κινητήρες εσωτερικής καύσης.

Γραφική αναπαράσταση ρευμάτων AC και DC

Η γραφική μέθοδος καθιστά δυνατή την οπτικοποίηση της διαδικασίας αλλαγής μιας συγκεκριμένης μεταβλητής ανάλογα με το χρόνο.

Η γραφική παράσταση μεταβλητών που αλλάζουν με την πάροδο του χρόνου ξεκινά με τη γραφική παράσταση δύο αμοιβαία κάθετων γραμμών που ονομάζονται άξονες του γραφήματος. Στη συνέχεια, στον οριζόντιο άξονα, σε μια συγκεκριμένη κλίμακα, απεικονίζονται χρονικά διαστήματα και στον κατακόρυφο άξονα, επίσης σε μια συγκεκριμένη κλίμακα, οι τιμές της προς αποτύπωση ποσότητας (EMF, τάση ή ρεύμα).

Στο σχ. 2 γραφικά συνεχούς ρεύματος και εναλλασσόμενου ρεύματος ... Σε αυτή την περίπτωση καθυστερούμε τις τρέχουσες τιμές και οι τιμές ρεύματος μιας κατεύθυνσης, που συνήθως ονομάζεται θετική, καθυστερούν κατακόρυφα από το σημείο τομής των αξόνων Ο , και κάτω από αυτό το σημείο, η αντίθετη κατεύθυνση, που συνήθως ονομάζεται αρνητική.

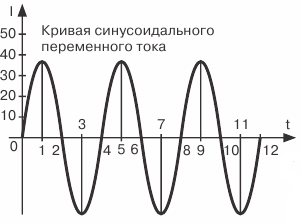Εικόνα 2. Γραφική αναπαράσταση DC και AC

Το ίδιο το σημείο O χρησιμεύει τόσο ως αφετηρία των σημερινών τιμών (κάθετα προς τα κάτω και πάνω) όσο και ως χρόνος (οριζόντια δεξιά).Με άλλα λόγια, αυτό το σημείο αντιστοιχεί στη μηδενική τιμή του ρεύματος και σε αυτό το σημείο εκκίνησης στο χρόνο από το οποίο σκοπεύουμε να εντοπίσουμε πώς θα αλλάξει το ρεύμα στο μέλλον.

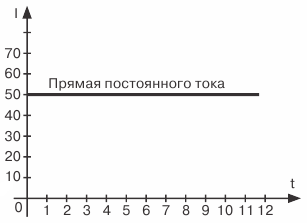
Ας επαληθεύσουμε την ορθότητα αυτού που απεικονίζεται στο σχ. 2 και μια γραφική παράσταση ρεύματος συνεχούς ρεύματος 50 mA.

Δεδομένου ότι αυτό το ρεύμα είναι σταθερό, δηλαδή, δεν αλλάζει το μέγεθος και την κατεύθυνσή του με την πάροδο του χρόνου, οι ίδιες τιμές ρεύματος θα αντιστοιχούν σε διαφορετικές χρονικές στιγμές, δηλαδή 50 mA. Επομένως, τη χρονική στιγμή ίση με το μηδέν, δηλαδή την αρχική στιγμή της παρατήρησής μας του ρεύματος, θα είναι ίσο με 50 mA. Σχεδιάζοντας ένα τμήμα ίσο με την τρέχουσα τιμή των 50 mA στον κατακόρυφο άξονα προς τα πάνω, παίρνουμε το πρώτο σημείο του γραφήματος μας.

Πρέπει να κάνουμε το ίδιο για την επόμενη χρονική στιγμή που αντιστοιχεί στο σημείο 1 στον άξονα του χρόνου, δηλαδή να αναβάλουμε από αυτό το σημείο κατακόρυφα προς τα πάνω ένα τμήμα επίσης ίσο με 50 mA. Το τέλος του τμήματος θα ορίσει το δεύτερο σημείο του γραφήματος για εμάς.

Έχοντας κάνει παρόμοια κατασκευή για πολλά επόμενα χρονικά σημεία, λαμβάνουμε μια σειρά σημείων, η σύνδεση των οποίων θα δώσει μια ευθεία γραμμή, η οποία είναι μια γραφική αναπαράσταση μιας σταθερής τιμής ρεύματος 50 mA.

Σχεδιάζοντας ένα μεταβλητό EMF

Ας προχωρήσουμε στη μελέτη μεταβλητής γραφικής παράστασης EMF... Στο σχ. 3, ένα πλαίσιο που περιστρέφεται σε ένα μαγνητικό πεδίο φαίνεται στο επάνω μέρος και μια γραφική αναπαράσταση της προκύπτουσας μεταβλητής EMF δίνεται παρακάτω.

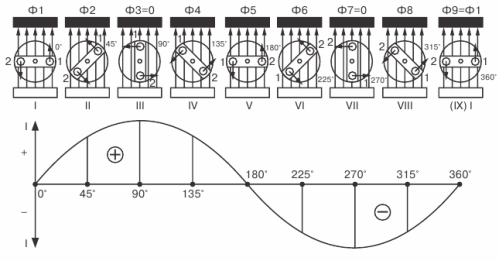Εικόνα 3. Σχεδίαση της μεταβλητής EMF

Αρχίζουμε να περιστρέφουμε ομοιόμορφα το πλαίσιο δεξιόστροφα και ακολουθούμε την πορεία των αλλαγών του EMF σε αυτό, παίρνοντας την οριζόντια θέση του πλαισίου ως αρχική στιγμή.

Σε αυτήν την αρχική στιγμή, το EMF θα είναι μηδέν επειδή οι πλευρές του πλαισίου δεν διασχίζουν τις γραμμές του μαγνητικού πεδίου.Στο γράφημα, αυτή η μηδενική τιμή του EMF που αντιστοιχεί στη στιγμή t = 0 αντιπροσωπεύεται από το σημείο 1.

Με περαιτέρω περιστροφή του πλαισίου, το EMF θα αρχίσει να εμφανίζεται σε αυτό και θα αυξάνεται μέχρι το πλαίσιο να φτάσει στην κατακόρυφη θέση του. Στο γράφημα, αυτή η αύξηση του EMF θα αντιπροσωπεύεται από μια ομαλή ανερχόμενη καμπύλη που φτάνει στην κορυφή της (σημείο 2).

Καθώς το πλαίσιο πλησιάζει στην οριζόντια θέση, το EMF σε αυτό θα μειωθεί και θα πέσει στο μηδέν. Στο γράφημα, αυτό θα απεικονιστεί ως μια ομαλή καμπύλη που πέφτει.

Επομένως, κατά τη διάρκεια του χρόνου που αντιστοιχεί σε μισή περιστροφή του πλαισίου, το EMF σε αυτό μπόρεσε να αυξηθεί από το μηδέν στη μέγιστη τιμή και να μειωθεί ξανά στο μηδέν (σημείο 3).

Με περαιτέρω περιστροφή του πλαισίου, το EMF θα επανεμφανιστεί σε αυτό και σταδιακά θα αυξηθεί σε μέγεθος, αλλά η κατεύθυνσή του θα αλλάξει ήδη προς το αντίθετο, όπως φαίνεται με την εφαρμογή του κανόνα του δεξιού χεριού.

Το γράφημα λαμβάνει υπόψη την αλλαγή στην κατεύθυνση του EMF, έτσι ώστε η καμπύλη που αντιπροσωπεύει το EMF να διασχίζει τον άξονα του χρόνου και τώρα να βρίσκεται κάτω από αυτόν τον άξονα. Το EMF αυξάνεται ξανά έως ότου το πλαίσιο πάρει κατακόρυφη θέση.

Τότε το EMF θα αρχίσει να μειώνεται και η τιμή του θα γίνει ίση με το μηδέν όταν το πλαίσιο επιστρέψει στην αρχική του θέση μετά την ολοκλήρωση μιας πλήρους περιστροφής. Στο γράφημα, αυτό θα εκφραστεί από το γεγονός ότι η καμπύλη EMF, φτάνοντας στην κορυφή της προς την αντίθετη κατεύθυνση (σημείο 4), θα συναντήσει στη συνέχεια τον άξονα του χρόνου (σημείο 5)

Αυτό ολοκληρώνει έναν κύκλο αλλαγής του EMF, αλλά αν συνεχίσετε την περιστροφή του πλαισίου, ο δεύτερος κύκλος ξεκινά αμέσως, επαναλαμβάνοντας ακριβώς τον πρώτο, ο οποίος με τη σειρά του θα ακολουθήσει ο τρίτος, μετά ο τέταρτος και ούτω καθεξής μέχρι να σταματήσουμε το πλαίσιο περιστροφής.

Έτσι, για κάθε περιστροφή του πλαισίου, το EMF που εμφανίζεται σε αυτό ολοκληρώνει έναν πλήρη κύκλο αλλαγής του.

Εάν το πλαίσιο είναι κλειστό σε κάποιο εξωτερικό κύκλωμα, τότε ένα εναλλασσόμενο ρεύμα θα ρέει μέσω του κυκλώματος, το γράφημα του οποίου θα μοιάζει με το γράφημα EMF.

Η κυματομορφή που προκύπτει ονομάζεται ημιτονοειδές κύμα και το ρεύμα, το EMF ή η τάση που ποικίλλει σύμφωνα με αυτόν τον νόμο ονομάζεται ημιτονοειδές.

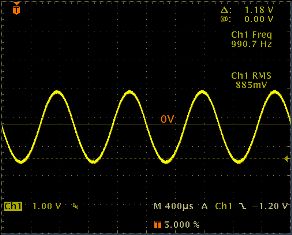
Η ίδια η καμπύλη ονομάζεται ημιτονοειδής επειδή είναι μια γραφική αναπαράσταση ενός μεταβλητού τριγωνομετρικού μεγέθους που ονομάζεται ημιτονοειδές.

Η ημιτονοειδής φύση της αλλαγής του ρεύματος είναι η πιο κοινή στην ηλεκτρική μηχανική, επομένως, μιλώντας για εναλλασσόμενο ρεύμα, στις περισσότερες περιπτώσεις σημαίνουν ημιτονοειδές ρεύμα.

Για να συγκρίνετε διαφορετικά εναλλασσόμενα ρεύματα (EMFs και τάσεις), υπάρχουν τιμές που χαρακτηρίζουν ένα συγκεκριμένο ρεύμα. Αυτές ονομάζονται παράμετροι AC.

Περίοδος, Πλάτος και Συχνότητα — Παράμετροι AC

Το εναλλασσόμενο ρεύμα χαρακτηρίζεται από δύο παραμέτρους - μηνιαίο κύκλο και πλάτος, γνωρίζοντας ποιες μπορούμε να υπολογίσουμε τι είδους εναλλασσόμενο ρεύμα είναι και να δημιουργήσουμε ένα γράφημα του ρεύματος.

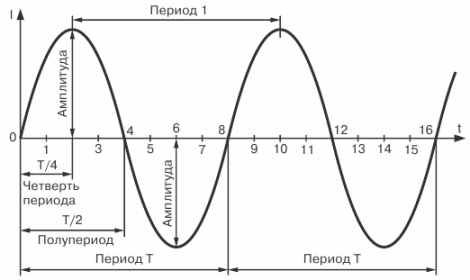
Εικόνα 4. Ημιτονοειδής καμπύλη ρεύματος

Η χρονική περίοδος κατά την οποία συμβαίνει ένας πλήρης κύκλος της τρέχουσας αλλαγής ονομάζεται περίοδος. Η περίοδος συμβολίζεται με το γράμμα Τ και μετριέται σε δευτερόλεπτα.

Η χρονική περίοδος κατά την οποία συμβαίνει το ήμισυ ενός πλήρους κύκλου μεταβολής του ρεύματος ονομάζεται μισός κύκλος Επομένως, η περίοδος μεταβολής του ρεύματος (EMF ή τάση) αποτελείται από δύο μισές περιόδους. Είναι προφανές ότι όλες οι περίοδοι του ίδιου εναλλασσόμενου ρεύματος είναι ίσες μεταξύ τους.

Όπως φαίνεται από το γράφημα, κατά τη διάρκεια μιας περιόδου μεταβολής του, το ρεύμα φθάνει το διπλάσιο της μέγιστης τιμής του.

Η μέγιστη τιμή ενός εναλλασσόμενου ρεύματος (EMF ή τάση) ονομάζεται τιμή πλάτους ή μέγιστου ρεύματος.

Τα Im, Em και Um είναι κοινές ονομασίες για τα πλάτη ρεύματος, EMF και τάσης.

Πρώτα απ 'όλα, δώσαμε προσοχή ρεύμα αιχμής, ωστόσο, όπως φαίνεται από το γράφημα, υπάρχουν αμέτρητες ενδιάμεσες τιμές που είναι μικρότερες από το πλάτος.

Η τιμή του εναλλασσόμενου ρεύματος (EMF, τάση) που αντιστοιχεί σε οποιαδήποτε επιλεγμένη χρονική στιγμή ονομάζεται στιγμιαία τιμή του.

Τα i, e και u είναι κοινώς αποδεκτοί προσδιορισμοί των στιγμιαίων τιμών του ρεύματος, του emf και της τάσης.

Η στιγμιαία τιμή του ρεύματος, καθώς και η μέγιστη τιμή του, είναι εύκολο να προσδιοριστεί με τη βοήθεια του γραφήματος. Για να το κάνετε αυτό, από οποιοδήποτε σημείο του οριζόντιου άξονα που αντιστοιχεί στο χρονικό σημείο που μας ενδιαφέρει, σχεδιάστε μια κάθετη γραμμή στο σημείο τομής με την τρέχουσα καμπύλη. το προκύπτον τμήμα της κάθετης γραμμής θα καθορίσει την τιμή του ρεύματος σε μια δεδομένη στιγμή, δηλαδή τη στιγμιαία τιμή του.

Προφανώς, η στιγμιαία τιμή του ρεύματος μετά το χρόνο T / 2 από το σημείο έναρξης του γραφήματος θα είναι μηδέν και μετά το χρόνο T / 4 η τιμή του πλάτους του. Το ρεύμα φθάνει επίσης τη μέγιστη τιμή του. αλλά ήδη προς την αντίθετη κατεύθυνση, μετά από χρόνο ίσο με 3/4 T.

Έτσι, το γράφημα δείχνει πώς το ρεύμα στο κύκλωμα αλλάζει με την πάροδο του χρόνου και ότι μόνο μια συγκεκριμένη τιμή τόσο του μεγέθους όσο και της κατεύθυνσης του ρεύματος αντιστοιχεί σε κάθε χρονική στιγμή. Σε αυτήν την περίπτωση, η τιμή του ρεύματος σε ένα δεδομένο χρονικό σημείο σε ένα σημείο του κυκλώματος θα είναι ακριβώς η ίδια σε οποιοδήποτε άλλο σημείο αυτού του κυκλώματος.

Ονομάζεται ο αριθμός των πλήρων περιόδων που πληρούνται από το ρεύμα σε 1 δευτερόλεπτο της συχνότητας AC και συμβολίζεται με το λατινικό γράμμα f.

Για να προσδιορίσετε τη συχνότητα ενός εναλλασσόμενου ρεύματος, δηλαδή, για να μάθετε πόσες περιόδους αλλαγής του έκανε το ρεύμα σε 1 δευτερόλεπτο, είναι απαραίτητο να διαιρέσετε 1 δευτερόλεπτο με το χρόνο μιας περιόδου f = 1 / T. Γνωρίζοντας τη συχνότητα του εναλλασσόμενου ρεύματος, μπορείτε να προσδιορίσετε την περίοδο: T = 1 / f

Συχνότητα AC μετριέται σε μια μονάδα που ονομάζεται hertz.

Αν έχουμε εναλλασσόμενο ρεύμα του οποίου η συχνότητα είναι ίση με 1 hertz, τότε η περίοδος ενός τέτοιου ρεύματος θα είναι ίση με 1 δευτερόλεπτο. Αντίστροφα, εάν η περίοδος μεταβολής του ρεύματος είναι 1 δευτερόλεπτο, τότε η συχνότητα ενός τέτοιου ρεύματος είναι 1 hertz.

Έτσι, ορίσαμε παραμέτρους εναλλασσόμενου ρεύματος —περίοδος, πλάτος και συχνότητα— που σας επιτρέπουν να διακρίνετε τα διαφορετικά ρεύματα εναλλασσόμενου ρεύματος, τα EMF και τις τάσεις και να σχεδιάζετε τα γραφήματα τους όταν χρειάζεται.

Κατά τον προσδιορισμό της αντίστασης διαφόρων κυκλωμάτων στο εναλλασσόμενο ρεύμα, χρησιμοποιήστε μια άλλη βοηθητική τιμή που χαρακτηρίζει το εναλλασσόμενο ρεύμα, το λεγόμενο γωνιακή ή γωνιακή συχνότητα.

Κυκλική συχνότητα που συμβολίζεται σε σχέση με τη συχνότητα f με την αναλογία 2 pif

Ας εξηγήσουμε αυτή την εξάρτηση. Κατά τη σχεδίαση του γραφήματος της μεταβλητής EMF, είδαμε ότι μια πλήρης περιστροφή του πλαισίου οδηγεί σε έναν πλήρη κύκλο αλλαγής EMF. Με άλλα λόγια, για να κάνει το πλαίσιο μία περιστροφή, δηλαδή να περιστραφεί 360 °, χρειάζεται χρόνος ίσος με μία περίοδο, δηλαδή T δευτερόλεπτα. Στη συνέχεια, σε 1 δευτερόλεπτο, το πλαίσιο κάνει μια περιστροφή 360 ° / T. Επομένως, 360 ° / T είναι η γωνία μέσω της οποίας το πλαίσιο περιστρέφεται σε 1 δευτερόλεπτο, και εκφράζει την ταχύτητα περιστροφής του πλαισίου, η οποία συνήθως ονομάζεται γωνιακή ή κυκλική ταχύτητα.

Αλλά επειδή η περίοδος T σχετίζεται με τη συχνότητα f με την αναλογία f = 1 / T, τότε η κυκλική ταχύτητα μπορεί επίσης να εκφραστεί ως συχνότητα και θα είναι ίση με 360 ° f.

Έτσι καταλήξαμε στο συμπέρασμα ότι 360 ° f. Ωστόσο, για την ευκολία χρήσης της κυκλικής συχνότητας για οποιουσδήποτε υπολογισμούς, η γωνία 360 ° που αντιστοιχεί σε μία περιστροφή αντικαθίσταται από μια ακτινική έκφραση ίση με ακτίνια 2pi, όπου pi = 3,14. Έτσι τελικά παίρνουμε 2pif. Επομένως, για να προσδιοριστεί η γωνιακή συχνότητα του εναλλασσόμενου ρεύματος (EMF ή τάση), πρέπει να πολλαπλασιάσετε τη συχνότητα σε hertz με έναν σταθερό αριθμό 6,28.