Θεωρία των αυτομάτων, πεπερασμένα αυτόματα
Η δομή, ο σχεδιασμός, η αρχή λειτουργίας διαφόρων μηχανών καθορίζονται σε μεγάλο βαθμό από τον λειτουργικό σκοπό του. Διάκριση μεταξύ τεχνολογικών, μεταφορών, υπολογιστών, στρατιωτικών και άλλων μηχανών. Ολόκληρα αυτόματα συγκροτήματα σχεδιασμένα να εκτελούν πολύπλοκες τεχνολογικές διεργασίες εισάγονται ευρέως σε διάφορες βιομηχανίες. Σχεδιάζονται και κατασκευάζονται αυτόματα που εκτελούν διάφορες λογικές λειτουργίες (λογικές μηχανές).
Θεωρία των αυτομάτων — τμήμα κυβερνητικής, που προέκυψαν υπό την επίδραση των απαιτήσεων της τεχνολογίας των ψηφιακών υπολογιστών και των μηχανών ελέγχου. Τα διακριτά αυτόματα που μελετώνται στη θεωρία των αυτομάτων είναι αφηρημένα μοντέλα πραγματικών συστημάτων (τεχνικών και βιολογικών) που επεξεργάζονται διακριτές (ψηφιακές) πληροφορίες σε διακριτά χρονικά βήματα.
Η θεωρία των αυτομάτων βασίζεται σε ακριβείς μαθηματικές έννοιες που επισημοποιούν διαισθητικές ιδέες σχετικά με τη λειτουργία (συμπεριφορά) του αυτόματου και για τη δομή του (εσωτερική δομή).
Σε αυτήν την περίπτωση, ο μετασχηματισμός πληροφοριών νοείται πάντα ως μια λειτουργία που μετατρέπει ακολουθίες εισόδου που αποτελούνται από γράμματα από το αλφάβητο εισόδου σε ακολουθίες εξόδου που αποτελούνται από γράμματα από το αλφάβητο εξόδου.
Η συσκευή της μαθηματικής λογικής, της άλγεβρας, της θεωρίας πιθανοτήτων, της συνδυαστικής και της θεωρίας γραφημάτων χρησιμοποιείται ευρέως.
Το πρόβλημα με τη θεωρία των αυτομάτων σε ορισμένα από τα μέρη της (δομική θεωρία των αυτομάτων) μεγάλωσε από τη θεωρία των κυκλωμάτων ρελέ-επαφής, που άρχισε να διαμορφώνεται στα τέλη της δεκαετίας του 1930. περιεκτικός μέθοδοι λογικής άλγεβρας.

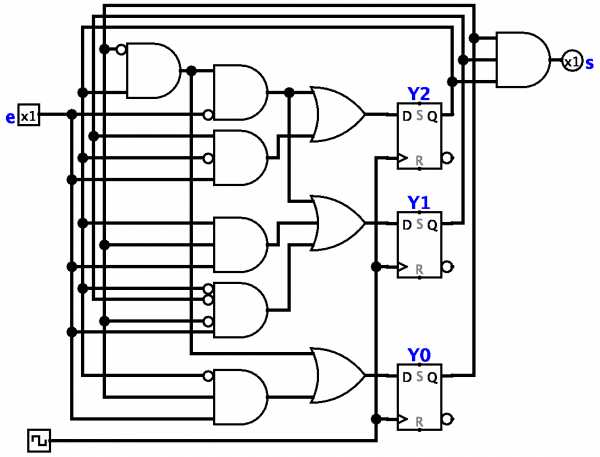
Στη δομική θεωρία των αυτομάτων, μελετώνται διαφορετικοί τύποι σχημάτων, σχεδιασμένων για να περιγράψουν πώς δημιουργείται ένα σύνθετο αυτόματο από απλούστερα στοιχεία (στοιχεία) σωστά συνδεδεμένα σε ένα σύστημα.
Μια άλλη κατεύθυνση, που ονομάζεται αφηρημένη θεωρία των αυτομάτων, μελετά τη συμπεριφορά των αυτομάτων (δηλαδή τη φύση του μετασχηματισμού των πληροφοριών που πραγματοποιούνται από αυτά), ενώ αφαιρείται από τις ιδιαιτερότητες της εσωτερικής τους δομής και προέκυψε τη δεκαετία του 1950.
Στο πλαίσιο της αφηρημένης θεωρίας των αυτομάτων, το περιεχόμενο των εννοιών «αυτόματο» και «μηχανή» εξαντλείται ουσιαστικά από την τυπική περιγραφή του μετασχηματισμού της πληροφορίας που πραγματοποιείται από ένα αυτόματο. Ένας τέτοιος μετασχηματισμός μπορεί να είναι ντετερμινιστικός, αλλά μπορεί επίσης να είναι πιθανολογικός.
Οι πιο μελετημένες είναι οι ντετερμινιστικές μηχανές (αυτόματα), οι οποίες περιλαμβάνουν πεπερασμένα αυτόματα - το κύριο αντικείμενο μελέτης στη θεωρία των αυτομάτων.
Μια μηχανή πεπερασμένης κατάστασης χαρακτηρίζεται από περιορισμένη ποσότητα μνήμης (ο αριθμός των εσωτερικών καταστάσεων) και ορίζεται χρησιμοποιώντας μια συνάρτηση μετάβασης.Με κάποια λογική εξιδανίκευση, όλες οι σύγχρονες μαθηματικές μηχανές, ακόμη και ο εγκέφαλος, από την άποψη της λειτουργίας τους, μπορούν να θεωρηθούν ως πεπερασμένα αυτόματα.
Οι όροι "διαδοχική μηχανή", "Milly automaton", "Moore automaton" χρησιμοποιούνται στη βιβλιογραφία (και όχι ομοιόμορφα από όλους τους συγγραφείς) ως συνώνυμα του όρου "πεπερασμένο αυτόματο" ή για να τονίσουν ορισμένα χαρακτηριστικά στις συναρτήσεις μετάβασης ενός πεπερασμένου αυτόματο.
Τα Automata με απεριόριστη μνήμη είναι μια μηχανή Turing ικανή να εκτελεί (δυνητικά) οποιονδήποτε αποτελεσματικό μετασχηματισμό πληροφοριών. Η έννοια της «μηχανής Turing» προέκυψε νωρίτερα από την έννοια της «μηχανής πεπερασμένης κατάστασης» και μελετάται κυρίως στη θεωρία των αλγορίθμων.
Η θεωρία των αφηρημένων αυτομάτων σχετίζεται στενά με γνωστές αλγεβρικές θεωρίες, για παράδειγμα τη θεωρία ημιομάδων. Από εφαρμοσμένης σκοπιάς, ενδιαφέρον παρουσιάζουν τα αποτελέσματα που χαρακτηρίζουν τη μετατροπή πληροφοριών σε ένα αυτόματο ως προς το μέγεθος της μνήμης.
Αυτό συμβαίνει, για παράδειγμα, σε προβλήματα με πειράματα σε αυτόματα (έργα του E.F. Moore, κ.λπ.), όπου η μία ή η άλλη πληροφορία για τις λειτουργίες μετάβασης του αυτόματου ή για τη χωρητικότητα της μνήμης του λαμβάνονται από τα αποτελέσματα του πειράματα.
Μια άλλη εργασία είναι ο υπολογισμός των περιόδων των ακολουθιών εξόδου, με βάση τις διαθέσιμες πληροφορίες σχετικά με το μέγεθος της μνήμης του αυτόματου και τις περιόδους των ακολουθιών εισόδου.
Μεγάλη σημασία έχει η ανάπτυξη μεθόδων για την ελαχιστοποίηση της μνήμης των μηχανών πεπερασμένης κατάστασης και τη μελέτη της συμπεριφοράς τους σε τυχαία περιβάλλοντα.
Στη θεωρία των αφηρημένων αυτομάτων, το πρόβλημα σύνθεσης είναι το εξής.Όσον αφορά κάποια σαφώς επισημοποιημένη γλώσσα, γράφονται οι προϋποθέσεις για τη συμπεριφορά του σχεδιασμένου αυτόματου (για το γεγονός που αναπαρίσταται στο αυτόματο). Σε αυτή την περίπτωση, είναι απαραίτητο να αναπτυχθούν μέθοδοι που σύμφωνα με κάθε γραπτή συνθήκη:
1) Μάθετε εάν υπάρχει μια τέτοια μηχανή κατάστασης που οι πληροφορίες που μετασχηματίζονται από αυτήν πληρούν αυτήν την προϋπόθεση.
2) εάν ναι, τότε οι συναρτήσεις μετάβασης μιας τέτοιας μηχανής πεπερασμένης κατάστασης κατασκευάζονται ή υπολογίζεται το μέγεθος της μνήμης της.
Η λύση του έργου σύνθεσης σε μια τέτοια διατύπωση προϋποθέτει την προκαταρκτική δημιουργία μιας βολικής γλώσσας για την καταγραφή των συνθηκών λειτουργίας ενός αυτόματου με βολικούς αλγόριθμους για τη μετάβαση από την εγγραφή στις μεταβατικές συναρτήσεις.
Στη δομική θεωρία των αυτομάτων, το πρόβλημα σύνθεσης συνίσταται στην κατασκευή μιας αλυσίδας στοιχείων ενός δεδομένου τύπου που πραγματοποιεί ένα πεπερασμένο αυτόματο που δίνεται από τις συναρτήσεις μετάβασής του. Σε αυτή την περίπτωση, συνήθως δηλώνουν κάποιο κριτήριο βελτιστοποίησης (για παράδειγμα, τον ελάχιστο αριθμό στοιχείων) και επιδιώκουν να αποκτήσουν ένα βέλτιστο σχήμα.
Όπως αποδείχθηκε αργότερα, αυτό σημαίνει ότι ορισμένες από τις μεθόδους και τις έννοιες που αναπτύχθηκαν νωρίτερα σε σχέση με κυκλώματα επαφής ρελέ είναι εφαρμόσιμες σε κυκλώματα άλλου τύπου.
Σε σχέση με την ανάπτυξη των ηλεκτρονικών τεχνολογιών, τα πιο διαδεδομένα είναι τα σχήματα λειτουργικών στοιχείων (λογικά δίκτυα). Μια ειδική περίπτωση λογικών δικτύων είναι τα αφηρημένα νευρωνικά δίκτυα, των οποίων τα στοιχεία ονομάζονται νευρώνες.
Έχουν αναπτυχθεί πολλές μέθοδοι σύνθεσης, ανάλογα με τον τύπο των κυκλωμάτων και τον μετασχηματισμό της πληροφορίας για την οποία προορίζονται (Σύνθεση συσκευών αναμετάδοσης).
Κοίτα -Ελαχιστοποίηση συνδυαστικών κυκλωμάτων, χάρτες Carnot, σύνθεση κυκλωμάτων
Μηχανή πεπερασμένης κατάστασης — ένα μαθηματικό μοντέλο συστήματος ελέγχου με σταθερό (δεν μπορεί να αυξηθεί κατά τη λειτουργία) μέγεθος μνήμης.
Η έννοια μιας μηχανής πεπερασμένης κατάστασης είναι μια μαθηματική αφαίρεση που χαρακτηρίζει τα γενικά χαρακτηριστικά ενός συνόλου συστημάτων ελέγχου (για παράδειγμα, μια συσκευή ρελέ πολλαπλών βρόχων). Όλα αυτά τα συστήματα έχουν κοινά χαρακτηριστικά που είναι φυσικό να δεχόμαστε ως ορισμό ενός πεπερασμένου αυτόματου.
Κάθε ολοκληρωμένο αυτόματο έχει μια είσοδο εκτεθειμένη σε εξωτερικές επιρροές και εσωτερικά στοιχεία. Τόσο για τα στοιχεία εισόδου όσο και για τα εσωτερικά στοιχεία, υπάρχει ένας σταθερός αριθμός διακριτών καταστάσεων που μπορούν να λάβουν.
Η αλλαγή στις καταστάσεις των στοιχείων εισόδου και των εσωτερικών στοιχείων συμβαίνει σε διακριτές χρονικές στιγμές, τα διαστήματα μεταξύ των οποίων ονομάζονται τικ. Η εσωτερική κατάσταση (η κατάσταση των εσωτερικών) στο τέλος της ταινίας καθορίζεται εξ ολοκλήρου από την εσωτερική κατάσταση και την κατάσταση της εισόδου στην αρχή της ταινίας.
Όλοι οι άλλοι ορισμοί ενός πεπερασμένου αυτόματου μπορούν να περιοριστούν σε αυτό το χαρακτηριστικό, ιδιαίτερα οι ορισμοί που υποθέτουν ότι ένα πεπερασμένο αυτόματο έχει μια έξοδο που εξαρτάται από την εσωτερική κατάσταση του αυτόματου σε μια δεδομένη στιγμή.
Όσον αφορά ένα τέτοιο χαρακτηριστικό, η φύση των εισόδων και των εσωτερικών καταστάσεων του είναι άσχετη με την περιγραφή ενός πλήρους αυτομάτου. Αντί για εισόδους και καταστάσεις, μπορείτε απλώς να δείτε τους αριθμούς τους σε τυχαία αρίθμηση.
Η μηχανή κατάστασης θα οριστεί εάν καθοριστεί η εξάρτηση του αριθμού της εσωτερικής κατάστασης από τον προηγούμενο αριθμό εσωτερικής κατάστασης και τον προηγούμενο αριθμό κατάστασης εισόδου. Μια τέτοια εργασία μπορεί να έχει τη μορφή τελικού πίνακα.
Ένας άλλος συνηθισμένος τρόπος για να ορίσετε ένα πλήρες αυτόματο είναι η κατασκευή του λεγόμενου διαγράμματα μετάβασης. Οι καταστάσεις εισόδου ονομάζονται συχνά απλά είσοδοι και οι εσωτερικές καταστάσεις είναι απλώς καταστάσεις.
Μια μηχανή πεπερασμένης κατάστασης μπορεί να είναι ένα μοντέλο τόσο τεχνικών συσκευών όσο και ορισμένων βιολογικών συστημάτων. Τα αυτόματα του πρώτου τύπου είναι, για παράδειγμα, συσκευές αναμετάδοσης και διάφοροι ηλεκτρονικοί υπολογιστές, συμπεριλαμβανομένων. προγραμματιζόμενοι λογικοί ελεγκτές.
Στην περίπτωση μιας συσκευής ρελέ, ο ρόλος των καταστάσεων εισόδου παίζεται από συνδυασμούς καταστάσεων των ευαίσθητων στοιχείων της συσκευής ρελέ (κάθε συνδυασμός τέτοιων καταστάσεων είναι μια «σύνθετη κατάσταση», που χαρακτηρίζεται από μια ένδειξη όλων των ευαίσθητων στοιχείων του αυτές οι διακριτές καταστάσεις που έχουν σε μια δεδομένη στιγμή). Ομοίως, συνδυασμοί καταστάσεων ενδιάμεσων στοιχείων μιας συσκευής ρελέ λειτουργούν ως εσωτερικές καταστάσεις.
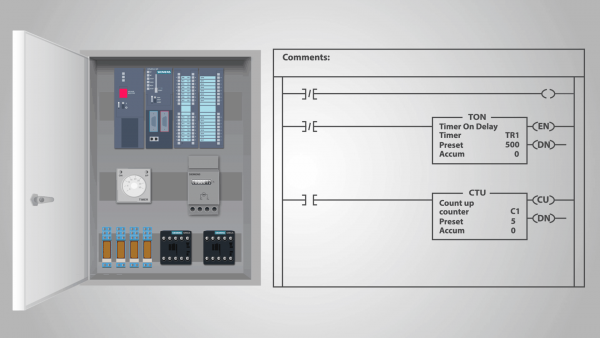
Ένας προγραμματιζόμενος λογικός ελεγκτής (PLC) είναι ένα παράδειγμα συσκευής δράσης ρελέ που μπορεί να ονομαστεί αυτόνομη μηχανή κατάστασης.
Στην πραγματικότητα, από τη στιγμή που το πρόγραμμα έχει εισαχθεί στο PLC και ο ελεγκτής έχει αρχίσει να υπολογίζει, δεν εκτίθεται σε εξωτερικές επιρροές και κάθε επόμενη κατάσταση καθορίζεται πλήρως από την προηγούμενη κατάστασή του. Μπορούμε να υποθέσουμε ότι η είσοδος έχει την ίδια κατάσταση σε κάθε κύκλο ρολογιού.
Αντίθετα, κάθε μηχανή πεπερασμένης κατάστασης που έχει τη μόνη δυνατή κατάσταση εισόδου ονομάζεται φυσικά αυτόνομη, αφού σε αυτή την περίπτωση το εξωτερικό περιβάλλον δεν φέρει καμία πληροφορία που να ελέγχει τη συμπεριφορά του.
Δείτε επίσης:
Η χρήση συστημάτων μικροεπεξεργαστή στην ηλεκτρική μηχανική στο παράδειγμα της χρήσης PLC