Διαγράμματα σύνδεσης τριφασικών κυκλωμάτων σε ηλεκτρικά δίκτυα

Τα πλεονεκτήματα των τριφασικών δικτύων, διασφαλίζοντας την ευρεία διανομή τους, είναι προφανή:

• Η ενέργεια μεταδίδεται με τρία καλώδια σε μεγάλες αποστάσεις πιο οικονομικά από ό,τι αν υπήρχαν λιγότερες φάσεις.

• σύγχρονες γεννήτριες, ασύγχρονοι κινητήρες, μετασχηματιστές τριών φάσεων — εύκολος στην κατασκευή, οικονομικός και αξιόπιστος στη λειτουργία.

• Τέλος, ένα τριφασικό σύστημα εναλλασσόμενου ρεύματος έχει τη δυνατότητα να παρέχει (και να παίρνει) σταθερή στιγμιαία ισχύ για μια περίοδο ημιτονοειδούς ρεύματος εάν το φορτίο της τριφασικής γεννήτριας είναι το ίδιο σε όλες τις φάσεις.

Ας δούμε ποια βασικά τριφασικά κυκλώματα υπάρχουν στα ηλεκτρικά δίκτυα.

Οι περιελίξεις ενός τριφασικού εναλλάκτη μπορούν γενικά να συνδεθούν με φορτία με διάφορους τρόπους. Έτσι, ο πιο οικονομικός τρόπος θα ήταν να συνδέσετε απευθείας ένα ξεχωριστό φορτίο σε κάθε φάση της γεννήτριας, επεκτείνοντας δύο καλώδια για κάθε φορτίο. Αλλά με αυτήν την προσέγγιση, θα χρειαστούν έξι καλώδια για τη σύνδεση.

Αυτό είναι πολύ σπατάλη από άποψη κατανάλωσης υλικού και άβολο.Για να επιτευχθεί εξοικονόμηση υλικού, οι περιελίξεις μιας τριφασικής γεννήτριας απλώς συνδυάζονται σε ένα κύκλωμα «αστέρι» ή «δέλτα». Με αυτή τη λύση καλωδίωσης, λαμβάνονται το μέγιστο 4 ("αστέρι με σημείο μηδέν" ή "δέλτα") ή ένα ελάχιστο 3.

Μια τριφασική γεννήτρια απεικονίζεται σε διαγράμματα με τη μορφή τριών περιελίξεων που βρίσκονται σε γωνίες 120 ° μεταξύ τους. Εάν η σύνδεση των περιελίξεων της γεννήτριας πραγματοποιείται σύμφωνα με το σχήμα "αστέρι", τότε οι ακροδέκτες με το ίδιο όνομα των περιελίξεων συνδέονται μεταξύ τους σε ένα σημείο (το λεγόμενο "σημείο μηδέν" της γεννήτριας ). Το σημείο μηδέν σημειώνεται με το γράμμα «O», και οι ελεύθεροι ακροδέκτες (ακροδέκτες φάσης) των περιελίξεων σημειώνονται με τα γράμματα «A», «B» και «C».

Εάν οι περιελίξεις της γεννήτριας συνδέονται μεταξύ τους σε ένα σχήμα "τριγώνου", τότε το τέλος της πρώτης περιέλιξης συνδέεται με την αρχή της δεύτερης περιέλιξης, το τέλος της δεύτερης περιέλιξης - στην αρχή της τρίτης τέλος του τρίτου - στην αρχή του πρώτου - το τρίγωνο είναι κλειστό. Γεωμετρικά, το άθροισμα του EMF σε ένα τέτοιο τρίγωνο θα είναι μηδέν. Και αν το φορτίο δεν είναι καθόλου συνδεδεμένο στους ακροδέκτες «A», «B» και «C», το ρεύμα δεν θα ρέει μέσω των περιελίξεων της γεννήτριας.

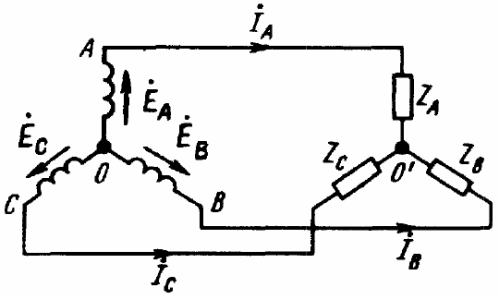
Ως αποτέλεσμα, έχουμε πέντε βασικά σχήματα για τη σύνδεση τριφασικής γεννήτριας με τριφασικό φορτίο (βλ. εικόνες). Μόνο σε τρία από αυτά τα σχήματα μπορείτε να δείτε ένα τριφασικό φορτίο συνδεδεμένο με αστέρι, όπου τα τρία άκρα του φορτίου συνδυάζονται σε ένα μόνο σημείο. Αυτό το σημείο στο κέντρο του αστεριού φορτίου ονομάζεται «σημείο μηδέν φορτίου» και φέρει την ένδειξη «Ο».

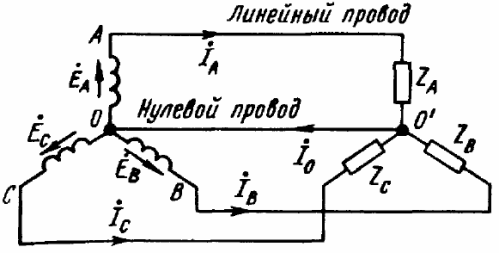
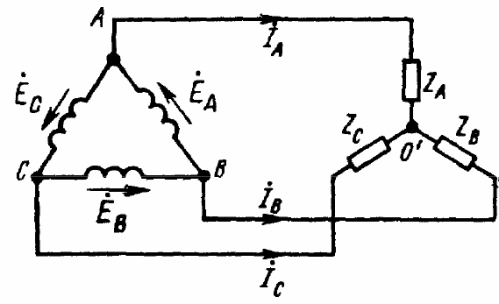
Ο αγωγός που συνδέει τα ουδέτερα σημεία του φορτίου και τη γεννήτρια ονομάζεται ουδέτερος αγωγός σε τέτοια κυκλώματα. Το ρεύμα του ουδέτερου καλωδίου συμβολίζεται ως «Io».Για τη θετική κατεύθυνση του ρεύματος συνήθως λαμβάνεται η κατεύθυνση από το φορτίο προς τη γεννήτρια, δηλαδή από το σημείο «Ο» στο σημείο «Ο».

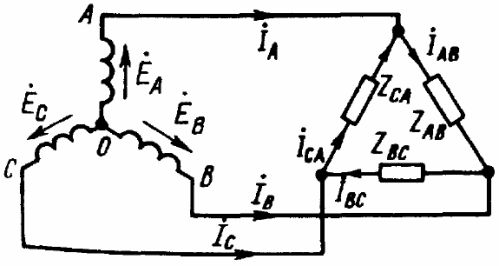
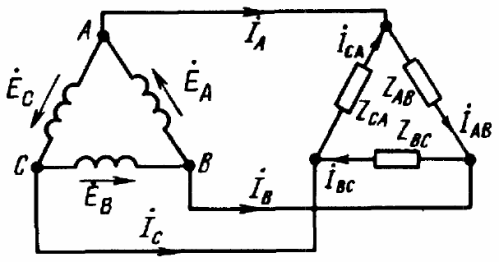
Τα καλώδια που συνδέουν τα σημεία "A", "B" και "C" των ακροδεκτών της γεννήτριας με το φορτίο ονομάζονται καλώδια γραμμής και τα κυκλώματα αντίστοιχα: αστέρι-αστέρι με ουδέτερο καλώδιο, αστέρι-αστέρας, αστέρι-τρίγωνο, δέλτα- δέλτα, δέλτα-αστέρι - μόνο πέντε βασικά σχήματα για τη σύνδεση τριφασικών κυκλωμάτων σε ηλεκτρικά δίκτυα.

Τα ρεύματα που διαρρέουν γραμμικούς αγωγούς ονομάζονται γραμμικά ρεύματα και συμβολίζονται με Ia, Ib, Ic. Για τη θετική κατεύθυνση του ρεύματος γραμμής, συνήθως λαμβάνεται η κατεύθυνση από τη γεννήτρια προς το φορτίο. Οι τιμές της μονάδας των ρευμάτων γραμμής σημαίνουν Il, κατά κανόνα, χωρίς πρόσθετους δείκτες, καθώς συμβαίνει συχνά όλα τα ρεύματα γραμμής του κυκλώματος είναι ίσα σε μέγεθος. Η τάση μεταξύ δύο γραμμικών αγωγών είναι η γραμμική τάση, που συμβολίζεται με Uab, Ubc, Uca ή, αν μιλάμε για ενότητα, γράφουν απλώς Ul.

Κάθε μία από τις περιελίξεις της γεννήτριας ονομάζεται φάση γεννήτριας και κάθε ένα από τα τρία μέρη ενός τριφασικού φορτίου ονομάζεται φάση φορτίου. Τα ρεύματα των φάσεων της γεννήτριας και, κατά συνέπεια, των φορτίων ονομάζονται ρεύματα φάσης, που συμβολίζονται με If. Οι εσωτερικές τάσεις των φάσεων της γεννήτριας και οι φάσεις φορτίου ονομάζονται τάσεις φάσης, συμβολίζονται Uf.

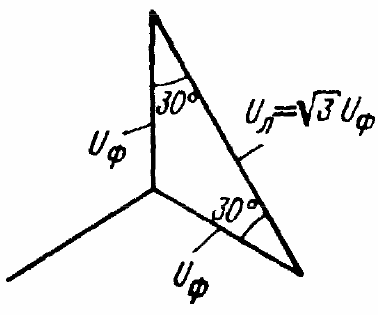
Εάν οι περιελίξεις της γεννήτριας συνδέονται σε ένα «αστέρι», τότε οι τάσεις της γραμμής είναι 3 φορές υψηλότερες από τη ρίζα (1,73 φορές) σε απόλυτη τιμή από τις τάσεις φάσης. Αυτό συμβαίνει επειδή οι τάσεις γραμμής θα γίνουν γεωμετρικά οι βάσεις ισοσκελές τριγώνων με οξείες γωνίες στη βάση των 30°, όπου τα σκέλη είναι οι τάσεις φάσης.Λάβετε υπόψη ότι μια σειρά από χαμηλές τριφασικές τάσεις: 127, 220, 380, 660 — σχηματίζεται απλώς πολλαπλασιάζοντας την προηγούμενη τιμή επί 1,73.

Όταν οι περιελίξεις της γεννήτριας συνδέονται σε "αστέρι", προφανώς το ρεύμα γραμμής είναι ίσο με το ρεύμα φάσης. Τι συμβαίνει όμως με τις τάσεις όταν οι περιελίξεις της γεννήτριας είναι συνδεδεμένες στο δέλτα; Στην περίπτωση αυτή, η τάση δικτύου θα είναι ίση με την τάση φάσης για κάθε φάση και για κάθε τμήμα του φορτίου: Ul = Uf. Όταν το φορτίο είναι συνδεδεμένο με αστέρι, το ρεύμα γραμμής θα είναι ίσο με το ρεύμα φάσης: Il = Αν.

Όταν το φορτίο συνδέεται σύμφωνα με το σχήμα "δέλτα", για τη θετική κατεύθυνση των ρευμάτων, επιλέξτε τη δεξιόστροφη κατεύθυνση της παράκαμψης δέλτα. Ο προσδιορισμός γίνεται από τους σχετικούς δείκτες: από ποιο σημείο ρέει το ρεύμα και σε ποιο σημείο ρέει, για παράδειγμα, Iab είναι ο προσδιορισμός του ρεύματος από το σημείο "Α" στο σημείο "Β".

Εάν ένα φορτίο τριών φάσεων είναι συνδεδεμένο σε δέλτα, τότε τα ρεύματα γραμμής και τα ρεύματα φάσης δεν θα είναι ίσα μεταξύ τους. Στη συνέχεια, τα ρεύματα γραμμής ανιχνεύονται από τα ρεύματα φάσης σύμφωνα με τον πρώτο νόμο του Kirchhoff: Ia = Iab-Ica, Ib = Ibc-Iab, Ic = Ica-Ibc.