Μέτρηση κυματομορφής και τάσης
 Το σχήμα των καμπυλών τάσης και ρεύματος θεωρείται πρακτικό ημιτονοειδής, εάν κάποια από τις τεταγμένες του διαφέρει από την αντίστοιχη τεταγμένη ενός ημιτονοειδούς ίσου σε πλάτος, με τμήμα που δεν υπερβαίνει το 5% του πλάτους.
Το σχήμα των καμπυλών τάσης και ρεύματος θεωρείται πρακτικό ημιτονοειδής, εάν κάποια από τις τεταγμένες του διαφέρει από την αντίστοιχη τεταγμένη ενός ημιτονοειδούς ίσου σε πλάτος, με τμήμα που δεν υπερβαίνει το 5% του πλάτους.
Η ημιτονικότητα μπορεί να ελεγχθεί με διάφορους τρόπους. Χρησιμοποιώντας την απλούστερη από αυτές, παρατηρήστε την καμπύλη που διερευνήθηκε στην οθόνη ενός παλμογράφου καθοδικών ακτίνων.
Για αυτό, δύο πανομοιότυπες ημιτονικές γραμμές σχεδιάζονται προηγουμένως στην οθόνη της συσκευής ή σε μια διαφανή πλάκα, μετατοπισμένες κάθετα μεταξύ τους κατά 10% του πλάτους τους (Εικ. 1).
Η υπό δοκιμή τάση εφαρμόζεται στη συνέχεια στην είσοδο Υ του παλμογράφου και ρυθμίζοντας το κέρδος στο κανάλι Υ και την περίοδο σάρωσης, μεγεθύνετε την καμπύλη οθόνης έτσι ώστε να βρίσκεται εντός της ζώνης που περιορίζεται από τα βοηθητικά ημιτονοειδή. Εάν αυτό πετύχει, τότε η τάση θεωρείται πρακτικά ημιτονοειδής.
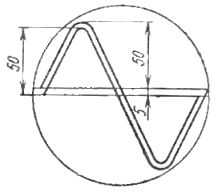
Ρύζι. 1. Βοηθητικές καμπύλες για τον προσδιορισμό του σχήματος ρεύματος και τάσης με χρήση παλμογράφου καθοδικών ακτίνων
Για να εξετάσουμε τον δεύτερο τρόπο προσδιορισμού της ημιτονικότητας μιας καμπύλης, εισάγουμε αρκετούς ορισμούς. Όπως γνωρίζετε, η τιμή μιας περιοδικής μεταβλητής μπορεί να χαρακτηριστεί από τις τιμές ενεργού, μέσου όρου και μέγιστου (πλάτους). Εάν το περιοδικό μέγεθος x αλλάζει σύμφωνα με έναν ημιτονοειδές νόμο, τότε όλες οι τιμές του σχετίζονται μεταξύ τους με συγκεκριμένο τρόπο.
Για παράδειγμα, ο λόγος της τιμής πλάτους προς την πραγματική τιμή, που ονομάζεται συντελεστής κορυφής ka = xm/ x = √2 = 1,41, ο λόγος της μέσης τιμής για μισή περίοδο προς την τιμή πλάτους, που ονομάζεται συντελεστής μέσης τιμής kCp = xcp / xm = 2 /π = 0,637 και τέλος ο λόγος της πραγματικής τιμής προς τη μέση τιμή, που ονομάζεται λόγος διαστάσεων ke = x / xCp = π / (2√2) = 1,11.
Εστιάζοντας σε αυτούς τους λόγους, το πρότυπο επιτρέπει τον προσδιορισμό του ημιτονοειδούς σχήματος της καμπύλης μιας περιοδικής ποσότητας με βάση τα αποτελέσματα της ταυτόχρονης μέτρησης του μέσου όρου και των ενεργών τιμών. Η καμπύλη θεωρείται σχεδόν ημιτονοειδής εάν 1,132> kph> 1,088.
Λόγω του γεγονότος ότι τα περισσότερα από τα όργανα μέτρησης που χρησιμοποιούνται στην πράξη είναι βαθμονομημένα σε μέσες τιμές, δεν είναι πάντα δυνατή η απευθείας μέτρηση της μέσης και της διάμεσης τιμής. Στην περίπτωση αυτή, η διερευνούμενη τιμή μετράται ταυτόχρονα με πλάτος (κορυφή) και ηλεκτροδυναμικά βολτόμετρα. Εάν είναι απαραίτητο να προσδιοριστούν και οι τρεις ονομασμένοι συντελεστές, θα πρέπει να συνδεθεί ένα βολτόμετρο ανορθωτή.
Οι ενδείξεις του βολτόμετρου και οι συντελεστές που χαρακτηρίζουν την ημιτονικότητα της φόρμας σχετίζονται με τις ακόλουθες αναλογίες: ka = 1,41U1/ U2, кf = U2/0,9U3, kcp = 0,673 = U3/ U1, όπου U1, U2, U3 — μετρήσεις πλάτους, ηλεκτροδυναμικής κλίμακας και βολτόμετρων ανορθωτικής κλίμακας βαθμονομημένες σε μέσες τιμές ημιτονοειδούς τάσης.
Ενα παράδειγμα. Για τον προσδιορισμό του μη ημιτονοειδούς σχήματος της καμπύλης τάσης της δευτερεύουσας περιέλιξης του μετασχηματιστή, η τάση φάσης μετράται ταυτόχρονα με βολτόμετρα πλάτους V3-43, ηλεκτροδυναμικά D-556 και ανορθωτή Ts4317.
Οι ενδείξεις τους ήταν U1 = 76 V, U2 = 61 V, U3 = 59,5 V. Τότε ka = 1,41 x 76/61 = 1,76, ke = 1,11 x 61 / 59,5 = 1, 14, kcp = 0,637 x 59,5 / 7.
Λόγω του γεγονότος ότι για μια ημιτονοειδή καμπύλη, αυτοί οι συντελεστές πρέπει να είναι 1,41, 1,11 και 0,637, αντίστοιχα, μπορεί να συναχθεί το συμπέρασμα ότι η τάση της δευτερεύουσας περιέλιξης του μετασχηματιστή έχει μη ημιτονοειδή μορφή. Δώστε προσοχή στο γεγονός ότι με ημιτονοειδή τάση, οι ενδείξεις και των τριών βολτόμετρων πρέπει να είναι ίσες.
