Η αρχή και οι μέθοδοι έμμεσου προσδιορισμού του συντελεστή ισχύος στο κύκλωμα εναλλασσόμενου ρεύματος

Συντελεστής ισχύος ή συνημίτονο phi, σε σχέση με τον χρήστη ημιτονοειδούς εναλλασσόμενου ρεύματος, είναι ο λόγος της ενεργού κατανάλωσης ισχύος P προς τη συνολική ισχύ S που παρέχεται σε αυτόν τον χρήστη από το δίκτυο.

Συνολική ισχύς S, στη γενική περίπτωση, μπορεί να οριστεί ως το γινόμενο των ενεργών τιμών (μέσο τετράγωνο ρίζας) του ρεύματος I και της τάσης U στο εξεταζόμενο κύκλωμα και της ενεργού ισχύος P — όπως καταναλώνεται αμετάκλητα από τον χρήστη για το λειτουργία της εργασίας.

Άεργος ισχύς Q, αν και αποτελεί μέρος της συνολικής ισχύος, ωστόσο, δεν καταναλώνεται για την εκτέλεση εργασιών, αλλά συμμετέχει μόνο στη δημιουργία εναλλασσόμενων ηλεκτρικών και μαγνητικών πεδίων σε ορισμένα στοιχεία του κυκλώματος του χρήστη.

εκτός άμεση μέτρηση συντελεστή ισχύος χρήση ηλεκτροδυναμικών συσκευών — μετρητές φάσης, υπάρχουν αρκετά λογικές έμμεσες μέθοδοι που σας επιτρέπουν να κατανοήσετε με μαθηματική ακρίβεια την τιμή αυτής της πολύ σημαντικής ηλεκτρικής ποσότητας που χαρακτηρίζει τον χρήστη σε ένα κύκλωμα ημιτονοειδούς εναλλασσόμενου ρεύματος.

Ας δούμε τα δεδομένα έμμεσες μεθόδους λεπτομερώς, Ας κατανοήσουμε την αρχή της έμμεσης μέτρησης του συντελεστή ισχύος.

Μέθοδος βολτόμετρου, αμπερόμετρου και βατόμετρου

Ηλεκτροδυναμικό βατόμετρο με πρόσθετη ενεργή αντίσταση στο κύκλωμα του κινούμενου πηνίου του υποδεικνύει την τιμή της εξαιρετικά ενεργής ισχύος που καταναλώνεται στο κύκλωμα AC P.

Εάν τώρα, χρησιμοποιώντας ένα βολτόμετρο και ένα αμπερόμετρο, μετρήσουμε τις μέσες τιμές του ρεύματος I και της τάσης U που ενεργεί στο κύκλωμα του υπό μελέτη φορτίου, τότε πολλαπλασιάζοντας αυτές τις δύο παραμέτρους, θα πάρουμε μόνο τη συνολική ισχύ S .

Τότε ο συντελεστής ισχύος (συνημίτονο phi) ενός δεδομένου φορτίου μπορεί εύκολα να βρεθεί χρησιμοποιώντας τον τύπο:

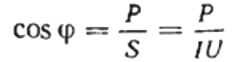
Εδώ, αν θέλετε, μπορείτε επίσης να βρείτε την τιμή της άεργου ισχύος Q, τη συνολική αντίσταση του κυκλώματος z Νόμος του Ohm, καθώς και ενεργητική και αντιδραστική αντίσταση, απλά κατασκευάζοντας ή αναπαριστώντας ένα τρίγωνο αντίστασης και στη συνέχεια χρησιμοποιώντας το Πυθαγόρειο θεώρημα:

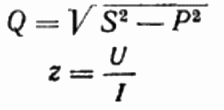
Μέθοδος μετρητή και αμπερόμετρου

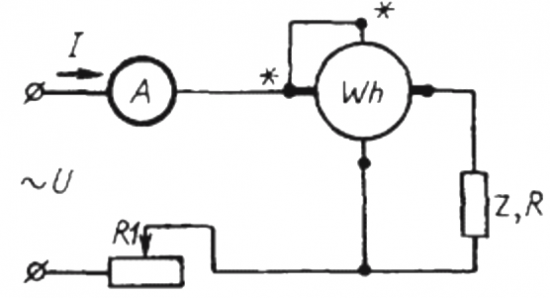
Για να χρησιμοποιήσετε αυτή τη μέθοδο, είναι απαραίτητο να συναρμολογήσετε ένα κύκλωμα στο οποίο το απλούστερο είναι συνδεδεμένο σε σειρά με το φορτίο Z και το αμπερόμετρο μετρητής ηλεκτρισμού Wh.

Για μια ορισμένη χρονική περίοδο t, της τάξεως ενός λεπτού, θα χρειαστεί να υπολογιστεί ο αριθμός των στροφών του δίσκου N, ο οποίος θα δείχνει την ποσότητα της ενεργού ενέργειας που δαπανήθηκε κατά τη διάρκεια ενός δεδομένου χρόνου (δηλ. λαμβάνοντας υπόψη την συντελεστής ισχύος).

Εδώ: ο αριθμός στροφών του δίσκου N, ο συντελεστής k είναι η ποσότητα ενέργειας ανά περιστροφή, I και U είναι το ρεύμα και η τάση rms αντίστοιχα, t είναι ο χρόνος μέτρησης των στροφών, το συνημίτονο phi είναι ο συντελεστής ισχύος:

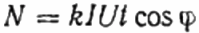
Στη συνέχεια, αντί του μελετώμενου χρήστη Z, το ενεργό φορτίο R περιλαμβάνεται στο κύκλωμα μέσω του ίδιου μετρητή, όχι όμως απευθείας, αλλά μέσω του ρεοστάτη R1 (επιτυγχάνοντας το ίδιο ρεύμα I όπως στην πρώτη περίπτωση, με τον χρήστη Z). Ο αριθμός των στροφών του δίσκου N1 διατηρείται για τον ίδιο χρόνο t. Αλλά εδώ, εφόσον το φορτίο είναι ενεργό, το συνημίτονο ph (συντελεστής ισχύος) είναι σίγουρα ίσο με 1. Επομένως:

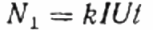
Στη συνέχεια, ο λόγος των στροφών του μετρητή δίσκου καταγράφεται για την ίδια χρονική περίοδο στην πρώτη και στη δεύτερη περίπτωση. Αυτό θα είναι συνημίτονο phi, δηλαδή ο συντελεστής ισχύος του πρώτου φορτίου (σε σχέση με ένα αμιγώς ενεργό φορτίο με το ίδιο ρεύμα):

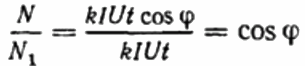
Μέθοδος τριών αμπερόμετρων

Για να προσδιορίσετε τον συντελεστή ισχύος σε ένα κύκλωμα ημιτονοειδούς ρεύματος χρησιμοποιώντας τρία αμπερόμετρα, πρέπει πρώτα να συναρμολογήσετε το ακόλουθο κύκλωμα:

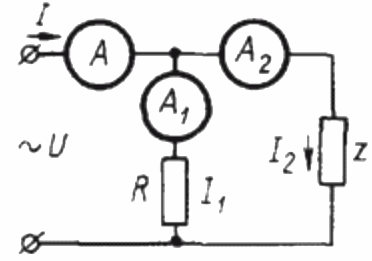
Εδώ το Z είναι ένα φορτίο του οποίου ο συντελεστής ισχύος πρέπει να προσδιοριστεί και το R είναι ένα καθαρά ενεργό φορτίο.

Δεδομένου ότι το φορτίο R είναι καθαρά ενεργό, το ρεύμα I1 σε οποιαδήποτε χρονική στιγμή βρίσκεται σε φάση με την εναλλασσόμενη τάση U που εφαρμόζεται σε αυτό το φορτίο. Στην περίπτωση αυτή, το ρεύμα I είναι ίσο με το γεωμετρικό άθροισμα των ρευμάτων I1 και I2. Τώρα θα δημιουργήσουμε με βάση αυτή τη θέση ένα διανυσματικό διάγραμμα των ρευμάτων:

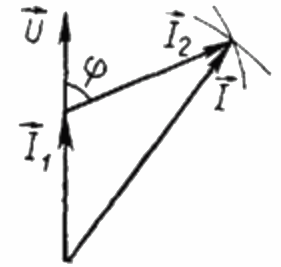
Στο διανυσματικό διάγραμμα των ρευμάτων, η οξεία γωνία μεταξύ του ρεύματος I1 και του ρεύματος I2 είναι η γωνία phi, το συνημίτονο της οποίας (στην πραγματικότητα, η τιμή του συντελεστή ισχύος) μπορεί να βρεθεί από έναν ειδικό πίνακα τιμών τριγωνομετρικών συναρτήσεων ή υπολογίζεται με τον τύπο:

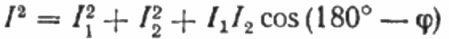
Από εδώ μπορούμε να εκφράσουμε το συνημίτονο phi, δηλαδή τον επιθυμητό συντελεστή ισχύος:

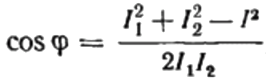
Το σύμβολο του συντελεστή ισχύος που βρέθηκε («+» ή «-«) θα υποδεικνύει τη φύση του φορτίου. Εάν ο συντελεστής ισχύος (συνημίτονο phi) είναι αρνητικός, το φορτίο έχει χωρητικό χαρακτήρα. Εάν ο συντελεστής ισχύος είναι θετική τιμή, τότε η φύση του φορτίου είναι επαγωγική.