Ηλεκτρομαγνητικές δονήσεις — χωρίς απόσβεση και εξαναγκασμένους κραδασμούς

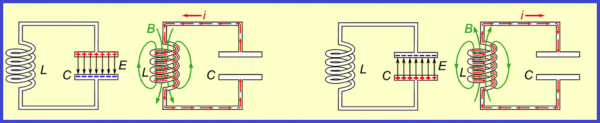
Οι ηλεκτρομαγνητικές δονήσεις σε ένα κύκλωμα που αποτελείται από έναν επαγωγέα και έναν πυκνωτή συμβαίνουν λόγω της περιοδικής μετατροπής της ηλεκτρικής ενέργειας σε μαγνητική ενέργεια και αντίστροφα. Σε αυτή την περίπτωση, το ηλεκτρικό φορτίο στις πλάκες του πυκνωτή και το μέγεθος του ρεύματος μέσω του πηνίου αλλάζουν περιοδικά.

Οι ηλεκτρομαγνητικές δονήσεις είναι ελεύθερες και εξαναγκασμένες. Οι ελεύθερες ταλαντώσεις, κατά κανόνα, αποσβένονται λόγω αντίστασης μη μηδενικού βρόχου και οι εξαναγκασμένες ταλαντώσεις είναι συνήθως αυτοταλαντώσεις.

Αποκτώ σε ένα δονούμενο κύκλωμα ελεύθερες ταλαντώσεις, πρέπει πρώτα να βγάλουμε αυτό το σύστημα από την ισορροπία: ενημερώστε τον πυκνωτή με μια αρχική φόρτιση q0 ή με κάποιο τρόπο εκκινήστε έναν παλμό ρεύματος I0 μέσω του πηνίου.

Αυτό θα χρησιμεύσει ως ένα είδος ώθησης και θα συμβούν ελεύθερες ηλεκτρομαγνητικές ταλαντώσεις στο κύκλωμα - θα ξεκινήσει η διαδικασία εναλλαγής φόρτισης και εκφόρτισης του πυκνωτή μέσω του επαγωγικού πηνίου και, κατά συνέπεια, η μεταβλητή άνοδος και πτώση του μαγνητικού πεδίου του πηνίου

Οι ταλαντώσεις που διατηρούνται σε ένα κύκλωμα από μια εξωτερική εναλλασσόμενη ηλεκτροκινητική δύναμη ονομάζονται εξαναγκασμένες ταλαντώσεις. Έτσι, όπως ήδη καταλάβατε, ένα παράδειγμα του απλούστερου ταλαντούμενου συστήματος στο οποίο μπορούν να παρατηρηθούν ελεύθερες ηλεκτρομαγνητικές ταλαντώσεις είναι ένα ταλαντούμενο κύκλωμα που αποτελείται από έναν πυκνωτή ηλεκτρικής χωρητικότητας C και ένα πηνίο επαγωγής L.

Σε ένα πραγματικό κύκλωμα ταλάντωσης, η διαδικασία επαναφόρτισης του πυκνωτή επαναλαμβάνεται περιοδικά, αλλά οι ταλαντώσεις εξαφανίζονται γρήγορα επειδή η ενέργεια διαχέεται κυρίως στην ενεργή αντίσταση R του σύρματος πηνίου.

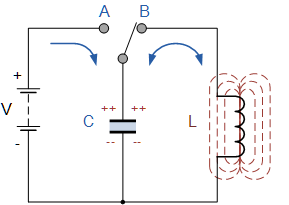
Θεωρήστε ένα κύκλωμα με ιδανικό κύκλωμα ταλάντωσης. Ας φορτίσουμε πρώτα τον πυκνωτή από την μπαταρία — θα του δώσουμε την αρχική φόρτιση q0, δηλαδή θα γεμίσουμε τον πυκνωτή με ενέργεια. Αυτή θα είναι η μέγιστη ενέργεια του πυκνωτή Εμείς.

Το επόμενο βήμα είναι να αποσυνδέσετε τον πυκνωτή από την μπαταρία και να τον συνδέσετε παράλληλα με το πηνίο. Σε αυτό το σημείο, ο πυκνωτής θα αρχίσει να εκφορτίζεται και ένα αυξανόμενο ρεύμα θα εμφανιστεί στο κύκλωμα του πηνίου. Όσο περισσότερο εκφορτίζεται ο πυκνωτής, τόσο περισσότερο φορτίο από αυτόν περνάει σταδιακά στο πηνίο, τόσο μεγαλύτερο γίνεται το ρεύμα στο πηνίο, επομένως το πηνίο αποθηκεύει ενέργεια με τη μορφή μαγνητικού πεδίου.

Αυτή η διαδικασία δεν γίνεται ακαριαία, αλλά σταδιακά, αφού το πηνίο έχει αυτεπαγωγή, που σημαίνει ότι συμβαίνει το φαινόμενο της αυτοεπαγωγής, που συνίσταται στο ότι το πηνίο ούτως ή άλλως αντιστέκεται στην αύξηση του ρεύματος. Σε κάποιο σημείο, η ενέργεια του μαγνητικού πεδίου του πηνίου φτάνει τη μέγιστη δυνατή τιμή Wm (ανάλογα με το πόσο φορτίο μεταφέρθηκε αρχικά στον πυκνωτή και ποια είναι η αντίσταση του κυκλώματος).

Επίσης, λόγω του φαινομένου της αυτοεπαγωγής, το ρεύμα διαμέσου του πηνίου διατηρείται στην ίδια κατεύθυνση, αλλά μειώνεται το μέγεθός του και τελικά το ηλεκτρικό φορτίο συσσωρεύεται ξανά στον πυκνωτή. Με αυτόν τον τρόπο, ο πυκνωτής επαναφορτίζεται. Οι πλάκες του έχουν πλέον αντίθετα σημάδια φόρτισης από ό,τι στην αρχή του πειράματος, όταν συνδέσαμε τον πυκνωτή με την μπαταρία.

Η ενέργεια του πυκνωτή έχει φτάσει τη μέγιστη δυνατή τιμή για αυτό το κύκλωμα. Το ρεύμα στο κύκλωμα έχει σταματήσει. Τώρα η διαδικασία αρχίζει να πηγαίνει προς την αντίθετη κατεύθυνση Και αυτό θα συνεχιστεί ξανά και ξανά, δηλαδή θα υπάρχουν ελεύθερες ηλεκτρομαγνητικές ταλαντώσεις.

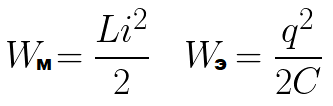
Εάν η ενεργή αντίσταση του κυκλώματος R είναι ίση με μηδέν, τότε η τάση στις πλάκες πυκνωτών και το ρεύμα μέσω του πηνίου θα ποικίλλουν άπειρα σύμφωνα με τον αρμονικό νόμο - συνημίτονο ή ημίτονο. Αυτό ονομάζεται αρμονική δόνηση. Το φορτίο στις πλάκες πυκνωτών θα άλλαζε επίσης σύμφωνα με έναν αρμονικό νόμο.

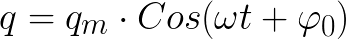
Δεν υπάρχει απώλεια στον ιδανικό κύκλο. Και αν ήταν, τότε η περίοδος των ελεύθερων ταλαντώσεων στο κύκλωμα θα εξαρτιόταν μόνο από την τιμή της χωρητικότητας C του πυκνωτή και της επαγωγής L του πηνίου. Αυτή η περίοδος μπορεί να βρεθεί (για έναν ιδανικό βρόχο με R = 0) χρησιμοποιώντας τον τύπο του Thomson:

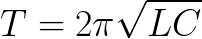
Η αντίστοιχη συχνότητα και συχνότητα κύκλου βρίσκονται για ένα ιδανικό κύκλωμα χωρίς απώλειες χρησιμοποιώντας τους ακόλουθους τύπους:

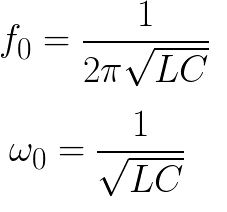
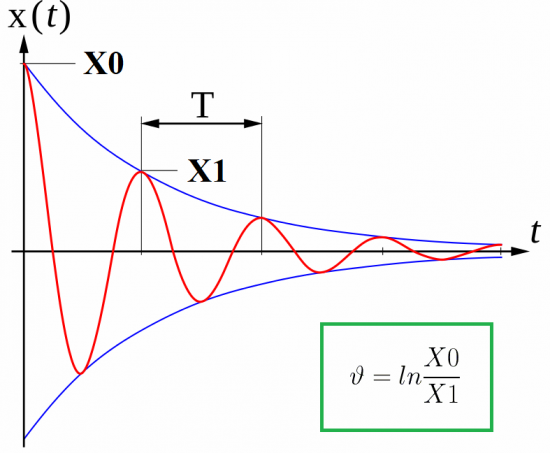
Όμως ιδανικά κυκλώματα δεν υπάρχουν και οι ηλεκτρομαγνητικές ταλαντώσεις αποσβένονται λόγω απωλειών λόγω θέρμανσης των καλωδίων. Ανάλογα με την τιμή της αντίστασης κυκλώματος R, κάθε επόμενη μέγιστη τάση πυκνωτή θα είναι χαμηλότερη από την προηγούμενη.

Σε σχέση με αυτό το φαινόμενο, μια τέτοια παράμετρος όπως η λογαριθμική μείωση των ταλαντώσεων ή η μείωση της απόσβεσης εισάγεται στη φυσική. Βρίσκεται ως ο φυσικός λογάριθμος του λόγου δύο διαδοχικών μεγίστων (του ίδιου πρόσημου) των ταλαντώσεων:

Η λογαριθμική μείωση της ταλάντωσης σχετίζεται με την ιδανική περίοδο ταλάντωσης με την ακόλουθη σχέση, όπου μπορεί να εισαχθεί μια πρόσθετη παράμετρος, η λεγόμενη Συντελεστής απόσβεσης:

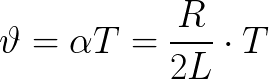
Η απόσβεση επηρεάζει τη συχνότητα των ελεύθερων κραδασμών. Επομένως, ο τύπος για την εύρεση της συχνότητας των ελεύθερων αποσβεσμένων ταλαντώσεων σε ένα πραγματικό κύκλωμα ταλάντωσης διαφέρει από τον τύπο για ένα ιδανικό κύκλωμα (λαμβάνεται υπόψη ο συντελεστής απόσβεσης):

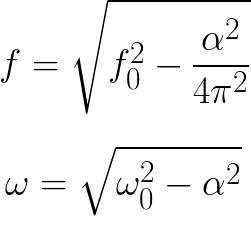
Να κάνει ταλαντώσεις στο κύκλωμα χωρίς σίγαση, είναι απαραίτητο να αναπληρώνονται και να αντισταθμίζονται αυτές οι απώλειες κάθε μισή περίοδο. Αυτό επιτυγχάνεται σε γεννήτριες συνεχούς ταλάντωσης, όπου η εξωτερική πηγή EMF αντισταθμίζει τις απώλειες θερμότητας με την ενέργειά της. Ένα τέτοιο σύστημα ταλαντώσεων με μια εξωτερική πηγή EMF ονομάζεται αυτοταλαντούμενο.