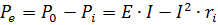Ισορροπία ισχύος σε ηλεκτρικό κύκλωμα
Σύμφωνα με Ο νόμος Joule-Lenz εργασία που γίνεται από συνεχές ρεύμα σε αντίσταση,
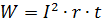
Εάν στον εξεταζόμενο κλάδο αντί για αντίσταση περιλαμβάνεται άλλος μετατροπέας ηλεκτρομαγνητικής ενέργειας σε μηχανική ή χημική ή άλλη μορφή ενέργειας (ηλεκτρικός κινητήρας, μπαταρία φόρτισης κ.λπ.), η εργασία που έγινε από το ρεύμα κατά τη διάρκεια του χρόνου t μπορεί να υπολογιστεί σε η περίπτωση που αν είναι γνωστή η τάση του μετατροπέα.
Σε αυτήν την περίπτωση, ο τύπος Joule-Lenz έχει διαφορετική μορφή:
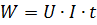
Σε συνεχές ρεύμα, η ισχύς που παρέχεται στο τμήμα του κυκλώματος με αντίσταση r δίνεται από την έκφραση:
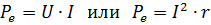
όπου τα I, U και r διατηρούν την ίδια σημασία όπως στον τύπο Joule-Lenz.
Η ισχύς που καταναλώνεται σε ολόκληρο το εξωτερικό κύκλωμα και η ισχύς που παρέχεται από τη γεννήτρια είναι ίδια. Η ισχύς που αναπτύσσεται από τη γεννήτρια είναι πάντα μεγαλύτερη από αυτή που δίνει η γεννήτρια στο εξωτερικό κύκλωμα, επειδή μέρος της ισχύος δαπανάται για την κάλυψη των απωλειών μέσα στην ίδια τη γεννήτρια.
Μια έκφραση ισοζυγίου ισχύος για έναν μόνο κλειστό βρόχο που περιέχει μια γεννήτρια με emf E και εσωτερική αντίσταση ri και μια αντίσταση αντίστασης r μπορεί να ληφθεί από την εξίσωση Kirchhoff.
Για αυτό το κύκλωμα
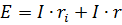
Εάν και οι δύο πλευρές αυτής της εξίσωσης πολλαπλασιαστούν με το ρεύμα στο κύκλωμα, τότε η εξίσωση που προκύπτει θα αντιπροσωπεύει το ισοζύγιο ισχύος σε αυτό το κύκλωμα
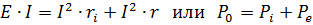
Η ισχύς που αναπτύσσεται από τη γεννήτρια ισούται με το άθροισμα της ισχύος που χάνεται μέσα στη γεννήτρια και δίνεται στο εξωτερικό κύκλωμα. P0 = EI είναι η ισχύς που αναπτύσσεται από τη γεννήτρια, Pe = UI = I2r είναι η ισχύς που δίνει η γεννήτρια στο εξωτερικό κύκλωμα και Pi — I2ri είναι η ισχύς που χάνεται μέσα στην ίδια τη γεννήτρια.
Όταν επιλέγετε τις ίδιες θετικές κατευθύνσεις του ρεύματος μέσω του ακροδέκτη διπλού άκρου I και της τάσης του ακροδέκτη διπλού άκρου U, η ισχύς που καταναλώνουν οι δύο ακροδέκτες, δηλαδή η διεπαφή χρήστη του προϊόντος, πρέπει να είναι θετική. Εάν ταυτόχρονα αποδειχθεί ότι η διεπαφή χρήστη του προϊόντος είναι αρνητική, αυτό θα σημαίνει ότι η συσκευή με δύο ακροδέκτες δεν καταναλώνει ηλεκτρομαγνητική ενέργεια, αλλά αντίθετα, είναι γεννήτρια ηλεκτρομαγνητικής ενέργειας και δίνει αυτή την ενέργεια σε ηλεκτρικό κύκλωμα.
Εάν σε ένα ηλεκτρικό κύκλωμα ένας αριθμός συσκευών με δύο ακροδέκτες εκπέμπει ηλεκτρομαγνητική ενέργεια στο κύκλωμα, οι υπόλοιπες απορροφούν αυτήν την ενέργεια. Σε ένα κύκλωμα συνεχούς ρεύματος, δεν μπορεί να συμβεί συσσώρευση ηλεκτρομαγνητικής ενέργειας. Επομένως, το άθροισμα της ισχύος που καταναλώνεται σε παθητικά δίκτυα δύο τερματικών και της ισχύος που χάνεται μέσα στις γεννήτριες πρέπει να είναι ίσο με το αλγεβρικό άθροισμα των δυνάμεων που αναπτύσσονται από όλες τις γεννήτριες, δηλ. το άθροισμα των προϊόντων EkIk όλων των γεννητριών που λειτουργούν σε ένα κύκλωμα:
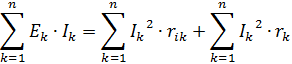
όπου n — ο αριθμός των κλαδιών στην αλυσίδα.
Η εξίσωση ισορροπίας που προκύπτει για ένα απλό κύκλωμα που περιέχει μία γεννήτρια μπορεί να ξαναγραφεί εκφράζοντας την ισχύ που καταναλώνεται στο εξωτερικό κύκλωμα ως την ισχύ που εκφράζεται από τη γεννήτρια και την ισχύ που χάνεται μέσα στη γεννήτρια: