Τιμές RMS ρεύματος και τάσης
Το εναλλασσόμενο ημιτονοειδές ρεύμα έχει διαφορετικές στιγμιαίες τιμές κατά τη διάρκεια της περιόδου. Είναι φυσικό να τεθεί το ερώτημα, ποια τιμή ρεύματος θα μετρηθεί με το αμπερόμετρο που περιλαμβάνεται στο κύκλωμα;
Κατά τον υπολογισμό των κυκλωμάτων εναλλασσόμενου ρεύματος, καθώς και των ηλεκτρικών μετρήσεων, δεν είναι βολικό να χρησιμοποιούνται στιγμιαίες τιμές ή τιμές πλάτους ρευμάτων και τάσεων και οι μέσες τιμές τους σε μια περίοδο είναι μηδέν. Επιπλέον, η ηλεκτρική επίδραση ενός περιοδικά μεταβαλλόμενου ρεύματος (η ποσότητα θερμότητας που απελευθερώνεται, η τέλεια λειτουργία κ.λπ.) δεν μπορεί να εκτιμηθεί από το πλάτος αυτού του ρεύματος.
Το πιο βολικό ήταν η εισαγωγή των εννοιών των λεγόμενων αποτελεσματικών τιμών ρεύματος και τάσης... Αυτές οι έννοιες βασίζονται στη θερμική (ή μηχανική) δράση του ρεύματος, η οποία δεν εξαρτάται από την κατεύθυνσή του.
Ρίζα μέση τετραγωνική τιμή εναλλασσόμενου ρεύματος - αυτή είναι η τιμή του συνεχούς ρεύματος στην οποία κατά τη διάρκεια της περιόδου εναλλασσόμενου ρεύματος απελευθερώνεται η ίδια ποσότητα θερμότητας στον αγωγό όπως κατά τη διάρκεια του εναλλασσόμενου ρεύματος.
Για την αξιολόγηση των ενεργειών που έγιναν εναλλασσόμενο ρεύμα, θα συγκρίνουμε τις δράσεις του με τη θερμική επίδραση του συνεχούς ρεύματος.
Η ισχύς συνεχούς ρεύματος P A που διέρχεται από την αντίσταση r θα είναι P = P2r.
Η ισχύς εναλλασσόμενου ρεύματος εκφράζεται ως η μέση επίδραση της στιγμιαίας ισχύος Az2r για ολόκληρη την περίοδο ή ο μέσος όρος των (I am x sinωT) 2 NS r για τον ίδιο χρόνο.
Έστω η μέση τιμή του t2 για την περίοδο M. Εξισώνοντας την ισχύ του συνεχούς ρεύματος και την ισχύ του εναλλασσόμενου ρεύματος, έχουμε: Az2r = Mr -n, από όπου Az = √M,
Η ποσότητα I ονομάζεται ενεργή τιμή του εναλλασσόμενου ρεύματος.
Η μέση τιμή του i2 σε εναλλασσόμενο ρεύμα προσδιορίζεται ως εξής.
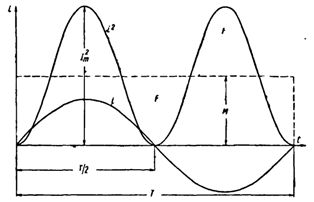
Ας κατασκευάσουμε μια ημιτονοειδή καμπύλη ρεύματος. Τετραγωνίζοντας κάθε τιμή στιγμιαίου ρεύματος, λαμβάνουμε μια καμπύλη P έναντι χρόνου.
AC τιμή rms
Και τα δύο μισά αυτής της καμπύλης βρίσκονται πάνω από τον οριζόντιο άξονα, καθώς τα αρνητικά ρεύματα (-i) στο δεύτερο μισό της περιόδου, όταν τετραγωνιστούν, δίνουν θετικές τιμές.
Κατασκευάστε ένα ορθογώνιο με βάση Τ και εμβαδόν ίσο με το εμβαδόν που οριοθετείται από την καμπύλη i2 και τον οριζόντιο άξονα. Το ύψος του ορθογωνίου M θα αντιστοιχεί στη μέση τιμή του P για την περίοδο. Αυτή η τιμή περιόδου, που υπολογίζεται χρησιμοποιώντας ανώτερα μαθηματικά, θα είναι ίση με 1/2 I2m... Επομένως, M. = 1/2 I2m
Εφόσον η τιμή rms Im εναλλασσόμενο ρεύμα είναι Im = √Mτότε τελικά I = Im / √2
Ομοίως, η σχέση μεταξύ των τιμών rms και πλάτους για την τάση U και E έχει τη μορφή:
U = Um / √2E = Em / √2
Οι ενεργές τιμές των μεταβλητών υποδεικνύονται με κεφαλαία γράμματα χωρίς δείκτες (I, U, E).
Με βάση τα παραπάνω, μπορούμε να πούμε ότι η πραγματική τιμή ενός εναλλασσόμενου ρεύματος είναι ίση με ένα τέτοιο συνεχές ρεύμα, το οποίο, περνώντας από την ίδια αντίσταση με το εναλλασσόμενο ρεύμα, απελευθερώνει την ίδια ποσότητα ενέργειας ταυτόχρονα.
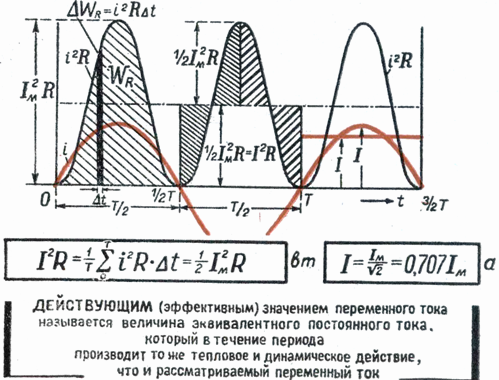
Τα ηλεκτρικά όργανα μέτρησης (αμπερόμετρα, βολτόμετρα) που περιλαμβάνονται σε ένα κύκλωμα εναλλασσόμενου ρεύματος υποδεικνύουν τις ενεργές τιμές του ρεύματος ή της τάσης.
Κατά την κατασκευή διανυσματικών διαγραμμάτων, είναι πιο βολικό να μην αναβάλλετε το πλάτος, αλλά τις αποτελεσματικές τιμές των διανυσμάτων. Για αυτό, τα μήκη των διανυσμάτων μειώνονται κατά √2 μία φορά. Αυτό δεν αλλάζει τη θέση των διανυσμάτων στο διάγραμμα.