Τριφασική παροχή ρεύματος: ενεργό, αντιδραστικό, πλήρες
Οι τιμές της συνολικής ενεργού και ολικής άεργου ισχύος του τριφασικού κυκλώματος είναι ίσες με τα αθροίσματα της ενεργού και άεργου ισχύος για καθεμία από τις τρεις φάσεις A, B και C, αντίστοιχα. Αυτή η δήλωση απεικονίζεται από τα ακόλουθα ΜΑΘΗΜΑΤΙΚΟΙ τυποι:
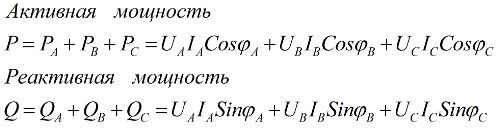
εδώ Ua, Ub, Uc, Ia, Ib, Ic είναι οι τιμές των τάσεων και των ρευμάτων φάσης και φ είναι η μετατόπιση φάσης.
Όταν το φορτίο είναι συμμετρικό, δηλαδή σε συνθήκες όπου η ενεργός και η άεργος ισχύς καθεμιάς από τις φάσεις είναι ίσες μεταξύ τους, για να βρεθεί η συνολική ισχύς του πολυφασικού κυκλώματος, αρκεί να πολλαπλασιάσουμε την τιμή της ισχύος φάσης με τον αριθμό των εμπλεκόμενων φάσεων. Η συνολική ισχύς προσδιορίζεται με βάση τις λαμβανόμενες τιμές των ενεργών και αντιδραστικών συστατικών του:
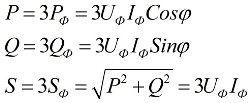
Στους παραπάνω τύπους, οι τιμές φάσης των ποσοτήτων μπορούν να εκφραστούν ως προς τις γραμμικές τους τιμές, οι οποίες θα διαφέρουν για τα σχήματα σύνδεσης αστεριού ή δέλτα για τους χρήστες, αλλά οι τύποι ισχύος θα είναι τελικά οι ίδιοι:
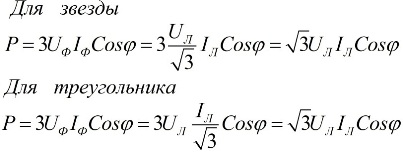
Από τις παραπάνω εκφράσεις προκύπτει ότι ανεξάρτητα από το σχήμα σύνδεσης των δεκτών ηλεκτρικής ενέργειας, είτε πρόκειται για τρίγωνο είτε για αστέρι, εάν το φορτίο είναι συμμετρικό, τότε οι τύποι για την εύρεση της ισχύος θα έχουν την ίδια μορφή, τόσο για τρίγωνο και για ένα αστέρι:
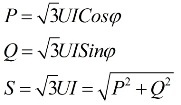
Αυτοί οι τύποι δείχνουν γραμμικές τιμές τάσης και ρεύματος και γράφονται χωρίς δείκτες. Συνήθως μια τέτοια σημείωση βρίσκεται, χωρίς δείκτες, δηλαδή αν δεν υπάρχουν δείκτες, τότε εννοούμε γραμμικές τιμές.
Μια ειδική συσκευή μέτρησης, που ονομάζεται βαττόμετρο… Οι ενδείξεις του καθορίζονται από τον τύπο:
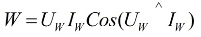
στον παραπάνω τύπο, Uw και Iw είναι τα διανύσματα της τάσης που εφαρμόζεται στο φορτίο και του ρεύματος που το διαρρέει.
Η φύση του ενεργού φορτίου και το διάγραμμα σύνδεσης φάσης μπορεί να διαφέρουν, επομένως, ανάλογα με τις συγκεκριμένες συνθήκες, τα διαγράμματα σύνδεσης του βατόμετρου θα είναι διαφορετικά.
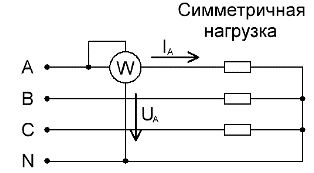
Για συμμετρικά φορτισμένα τριφασικά κυκλώματα, για μια πρόχειρη μέτρηση της συνολικής ενεργού ισχύος, εάν δεν απαιτείται υψηλή ακρίβεια, αρκεί ένα βατόμετρο συνδεδεμένο μόνο σε μία από τις φάσεις. Μετά από αυτό, για να λάβετε την τιμή της ενεργού ισχύος ολόκληρου του κυκλώματος, μένει να πολλαπλασιάσετε τις ενδείξεις του βατόμετρου με τον αριθμό των φάσεων:
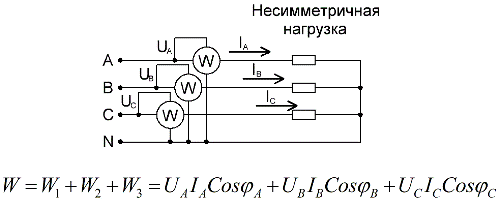
Για ένα κύκλωμα τεσσάρων συρμάτων με ουδέτερο καλώδιο, για την ακριβή μέτρηση της ενεργού ισχύος, απαιτούνται τρία βατόμετρα, καθένα από τα οποία διαβάζεται και στη συνέχεια αθροίζεται για να ληφθεί μια τιμή για τη συνολική ισχύ του κυκλώματος:
Εάν δεν υπάρχει ουδέτερο καλώδιο σε ένα τριφασικό κύκλωμα, τότε αρκούν δύο βατόμετρα για τη μέτρηση της συνολικής ισχύος, ακόμη και αν το φορτίο δεν είναι ισορροπημένο.
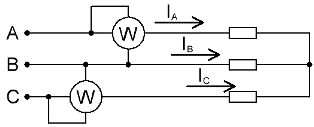
Ελλείψει ουδέτερου αγωγού, τα ρεύματα φάσης διασυνδέονται σύμφωνα με τον πρώτο νόμο του Kirchhoff:
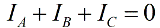
Τότε το άθροισμα των ενδείξεων ενός ζεύγους βατμέτρων θα είναι ίσο με:
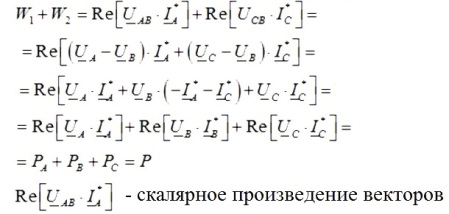
Έτσι, εάν προσθέσετε τις ενδείξεις ενός ζεύγους βατόμετρων, θα λάβετε τη συνολική ενεργή ισχύ στο υπό μελέτη κύκλωμα τριών φάσεων και οι ενδείξεις των βατόμετρων θα εξαρτηθούν τόσο από το μέγεθος του φορτίου όσο και από τη φύση του.
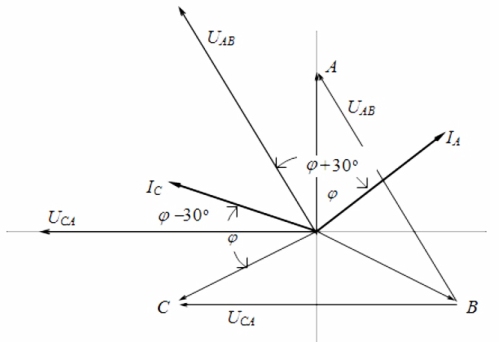
Εξετάζοντας το διανυσματικό διάγραμμα των ρευμάτων και των τάσεων σε σχέση με ένα συμμετρικό φορτίο, μπορεί να συναχθεί το συμπέρασμα ότι οι ενδείξεις των βατόμετρων καθορίζονται από τους ακόλουθους τύπους:
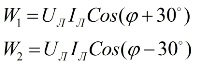
Μετά την ανάλυση αυτών των εκφράσεων, μπορεί να γίνει κατανοητό ότι με ένα καθαρά ενεργό φορτίο, όταν φ = 0, οι ενδείξεις των δύο βατόμετρων θα είναι ίσες μεταξύ τους, δηλαδή W1 = W2.
Με την αυτεπαγωγή ενεργού φορτίου, όταν 0 ≤ φ ≤ 90 °, οι ενδείξεις του βατόμετρου 1 θα είναι μικρότερες από αυτές του βατόμετρου 2, δηλαδή W1 60 °, οι ενδείξεις του βατόμετρου 1 θα είναι αρνητικές, δηλαδή W1 <0.
Με ενεργό-χωρητική φύση του φορτίου, όταν 0 ≥ φ≥ -90 °, οι ενδείξεις του βατόμετρου 2 θα είναι μικρότερες από το βατόμετρο 1, δηλαδή W1> W2. Σε φ <-60 °, οι ενδείξεις του βατόμετρου 2 θα γίνουν αρνητικές.
