Ηλεκτρικά κυκλώματα με μη ημιτονοειδή ρεύμα

Μη ημιτονοειδή ρεύματα και η αποσύνθεσή τους

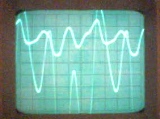Σε ένα ηλεκτρικό κύκλωμα, τα μη ημιτονοειδή ρεύματα μπορούν να συμβούν για δύο λόγους:

1. το ίδιο το ηλεκτρικό κύκλωμα είναι γραμμικό, αλλά μια μη ημιτονοειδής τάση δρα στο κύκλωμα,

2. η τάση που ενεργεί στο κύκλωμα είναι ημιτονοειδής, αλλά το ηλεκτρικό κύκλωμα περιέχει μη γραμμικά στοιχεία.

Μπορεί να υπάρχουν και οι δύο λόγοι. Αυτό το κεφάλαιο ασχολείται με τα κυκλώματα μόνο για το πρώτο σημείο. Στην περίπτωση αυτή, οι μη ημιτονικές τάσεις θεωρούνται περιοδικές.

Οι γεννήτριες περιοδικών παλμών χρησιμοποιούνται σε διάφορες συσκευές ραδιομηχανικής, αυτοματισμού, τηλεμηχανικής. Το σχήμα των παλμών μπορεί να είναι διαφορετικό: πριόνι, βαθμιδωτό, ορθογώνιο (Εικ. 1).

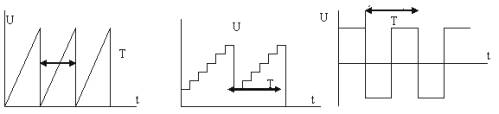
Εικόνα 1. Σχήματα παλμών

Τα φαινόμενα που συμβαίνουν σε ένα γραμμικό ηλεκτρικό κύκλωμα κάτω από περιοδικές αλλά μη ημιτονικές τάσεις είναι πιο εύκολο να μελετηθούν εάν η καμπύλη τάσης διαστέλλεται σε μια τριγωνομετρική σειρά Fourier:

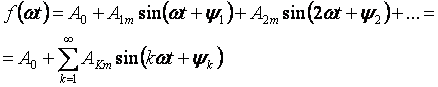
Ο πρώτος όρος της σειράς A0 ονομάζεται σταθερή συνιστώσα ή μηδενική αρμονική, ο δεύτερος όρος της σειράς

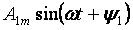
— η θεμελιώδης ή πρώτη αρμονική και όλα τα άλλα μέλη της μορφής

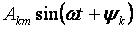
για k> 1 ονομάζονται ανώτερες αρμονικές.

Αν στην έκφραση (3.1) ανοίξουμε το ημίτονο του αθροίσματος, τότε μπορούμε να προχωρήσουμε σε άλλη μορφή γραφής της σειράς:

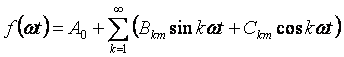Εάν η συνάρτηση είναι συμμετρική ως προς τον άξονα της τετμημένης, τότε η σειρά δεν περιέχει σταθερή συνιστώσα. Εάν η συνάρτηση είναι συμμετρική ως προς τον άξονα τεταγμένων, τότε η σειρά δεν περιέχει ημίτονο. Η συνάρτηση είναι συμμετρική ως προς την αρχή και δεν περιέχει συνημίτονο.

Μερικά παραδείγματα επέκτασης σειράς δίνονται σε έναν πίνακα. 1 και είναι επίσης διαθέσιμα στη βιβλιογραφία αναφοράς.

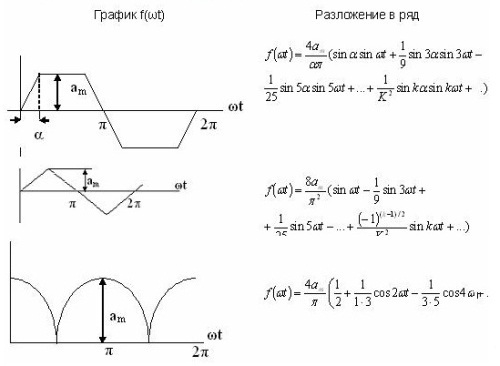
Πίνακας 1. Επέκταση σειράς Fourier

Υπολογισμός κυκλωμάτων μη ημιτονοειδούς ρεύματος

Το κύκλωμα υπολογίζεται για κάθε αρμονική σύμφωνα με το μοντέλο. Το κύκλωμα υπολογίζεται όσες φορές υπάρχουν αρμονικές στην τάση που ενεργούν στο κύκλωμα. Σε αυτή την περίπτωση, είναι απαραίτητο να ληφθούν υπόψη ορισμένα χαρακτηριστικά.

Πρέπει να σημειωθεί ότι η αντίσταση του επαγωγικού στοιχείου αυξάνεται όσο αυξάνεται ο αρμονικός αριθμός

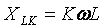
και το χωρητικό στοιχείο, αντίθετα, μειώνεται:

Θα πρέπει επίσης να ληφθεί υπόψη ότι η σταθερή συνιστώσα του ρεύματος δεν διέρχεται από τον πυκνωτή και η αυτεπαγωγή δεν είναι αντίσταση σε αυτόν.

Επιπλέον, δεν πρέπει να ξεχνάμε τα πιθανά φαινόμενα συντονισμού όχι μόνο στις θεμελιώδεις αρμονικές, αλλά και στις υψηλότερες αρμονικές.

Διανυσματικά διαγράμματα μπορεί να σχεδιαστεί για κάθε αρμονική χωριστά.

Σύμφωνα με την αρχή της υπέρθεσης, το ρεύμα κάθε κλάδου μπορεί να αποτελείται από το άθροισμα μεμονωμένων όρων (μηδέν, θεμελιώδεις και ανώτερες αρμονικές):

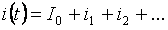
Η τιμή rms του συνολικού ρεύματος διακλάδωσης μπορεί να προσδιοριστεί από τη μέση τιμή των επιμέρους αρμονικών ρευμάτων:

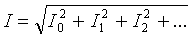
Η ενεργός ισχύς του μη ημιτονικού ρεύματος είναι ίση με το άθροισμα των ενεργών δυνάμεων των επιμέρους αρμονικών:

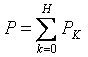
Παρακάτω είναι ένα γενικό παράδειγμα για τον υπολογισμό κυκλωμάτων μη ημιτονοειδούς ρεύματος. Όλα τα ρεύματα, οι τάσεις, οι αντιστάσεις θα έχουν δύο δείκτες: το πρώτο ψηφίο σημαίνει τον αριθμό διακλάδωσης και το δεύτερο ψηφίο τον αρμονικό αριθμό. Τάση εισόδου:

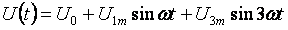
• Μόνιμο εξάρτημα

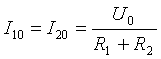
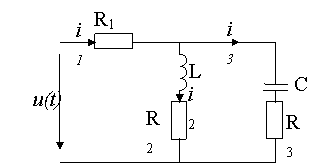
Εικόνα 2. Ηλεκτρικό διάγραμμα

• Κύρια αρμονική:

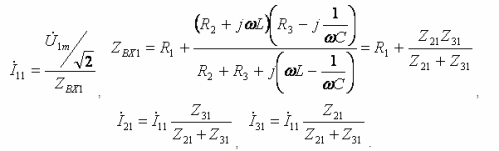
• Τρίτη αρμονική:

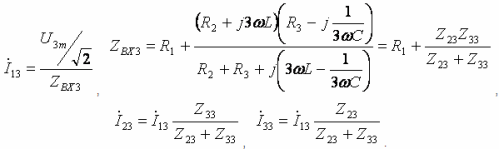
Διαβάστε επίσης: Τα πιο κοινά σχήματα διόρθωσης AC σε DC