Ενεργή αντίσταση και πηνίο σε κύκλωμα AC

Λαμβάνοντας υπόψη ένα κύκλωμα AC που περιέχει μόνο επαγωγική αντίσταση (δείτε το άρθρο «Πηνίο σε κύκλωμα εναλλασσόμενου ρεύματος»), υποθέσαμε ότι η ενεργή αντίσταση αυτού του κυκλώματος είναι μηδέν.

Στην πραγματικότητα, τόσο το ίδιο το καλώδιο του πηνίου όσο και τα καλώδια σύνδεσης έχουν μικρή αλλά ενεργή αντίσταση, οπότε το κύκλωμα καταναλώνει αναπόφευκτα την ενέργεια της πηγής ρεύματος.

Επομένως, κατά τον προσδιορισμό της συνολικής αντίστασης ενός εξωτερικού κυκλώματος, είναι απαραίτητο να προστεθούν οι αντιδραστικές και ενεργές αντιστάσεις του. Αλλά είναι αδύνατο να προστεθούν αυτές οι δύο αντιστάσεις που έχουν διαφορετική φύση.

Σε αυτή την περίπτωση, η σύνθετη αντίσταση του κυκλώματος στο εναλλασσόμενο ρεύμα βρίσκεται με γεωμετρική πρόσθεση.

Κατασκευάζεται ένα ορθογώνιο τρίγωνο (βλέπε σχήμα 1), του οποίου η μία πλευρά είναι η τιμή της επαγωγικής αντίστασης και η άλλη πλευρά είναι η τιμή της ενεργού αντίστασης. Η επιθυμητή σύνθετη αντίσταση κυκλώματος καθορίζεται από την τρίτη πλευρά του τριγώνου.

Σχήμα 1. Προσδιορισμός της σύνθετης αντίστασης ενός κυκλώματος που περιέχει επαγωγική και ενεργή αντίσταση

Η σύνθετη αντίσταση κυκλώματος συμβολίζεται με το λατινικό γράμμα Z και μετριέται σε ohms. Μπορεί να φανεί από την κατασκευή ότι η συνολική αντίσταση είναι πάντα μεγαλύτερη από την επαγωγική και την ενεργητική αντίσταση που λαμβάνονται χωριστά.

Η αλγεβρική έκφραση για τη συνολική αντίσταση κυκλώματος είναι:

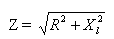
όπου Z — συνολική αντίσταση, R — ενεργή αντίσταση, XL — επαγωγική αντίσταση του κυκλώματος.

Επομένως, η συνολική αντίσταση ενός κυκλώματος στο εναλλασσόμενο ρεύμα, που αποτελείται από ενεργή και επαγωγική αντίσταση, είναι ίση με την τετραγωνική ρίζα του αθροίσματος των τετραγώνων της ενεργού και επαγωγικής αντίστασης αυτού του κυκλώματος.

Νόμος του Ohm αφού ένα τέτοιο κύκλωμα εκφράζεται με τον τύπο I = U / Z, όπου Z είναι η συνολική αντίσταση του κυκλώματος.

Ας αναλύσουμε τώρα ποια θα είναι η τάση εάν το κύκλωμα, εκτός από και και τη μετατόπιση φάσης μεταξύ του ρεύματος και της επαγωγής, έχει επίσης μια σχετικά μεγάλη ενεργό αντίσταση. Στην πράξη, ένα τέτοιο κύκλωμα μπορεί να είναι, για παράδειγμα, ένα κύκλωμα που περιέχει έναν επαγωγέα σιδήρου τυλιγμένο από ένα λεπτό σύρμα (τσοκ υψηλής συχνότητας).

Σε αυτήν την περίπτωση, η μετατόπιση φάσης μεταξύ ρεύματος και τάσης δεν θα είναι πλέον ένα τέταρτο της περιόδου (όπως ήταν σε ένα κύκλωμα με μόνο επαγωγική αντίσταση), αλλά πολύ λιγότερο. και όσο μεγαλύτερη είναι η αντίσταση, τόσο λιγότερη μετατόπιση φάσης θα προκύψει.

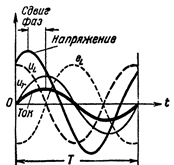
Εικόνα 2. Ρεύμα και τάση σε ένα κύκλωμα που περιέχει R και L.

Τώρα η ίδια EMF αυτοεπαγωγής δεν είναι σε αντιφάση με την τάση της πηγής ρεύματος, καθώς αντισταθμίζεται σε σχέση με την τάση όχι κατά μισή περίοδο, αλλά κατά λιγότερο.Επιπλέον, η τάση που δημιουργείται από την πηγή ρεύματος στους ακροδέκτες του πηνίου δεν είναι ίση με το emf της αυτοεπαγωγής, αλλά είναι μεγαλύτερη από αυτήν κατά την ποσότητα της πτώσης τάσης στην ενεργή αντίσταση του σύρματος του πηνίου. Με άλλα λόγια, η τάση στο πηνίο αποτελείται ούτως ή άλλως από δύο στοιχεία:

• tiL- το αντιδραστικό στοιχείο της τάσης, το οποίο εξισορροπεί την επίδραση του EMF από την αυτεπαγωγή,

• tiR- το ενεργό συστατικό της τάσης που θα ξεπεράσει την ενεργή αντίσταση του κυκλώματος.

Εάν συνδέσουμε μια μεγάλη ενεργή αντίσταση σε σειρά με το πηνίο, η μετατόπιση φάσης θα μειωθεί τόσο πολύ που το τρέχον ημιτονοειδές κύμα θα φτάσει σχεδόν το ημιτονοειδές κύμα τάσης και η διαφορά φάσεων μεταξύ τους θα είναι ελάχιστα αισθητή. το πλάτος του όρου και θα είναι μεγαλύτερο από το πλάτος του όρου.

Ομοίως, μπορείτε να μειώσετε τη μετατόπιση φάσης και ακόμη και να τη μειώσετε εντελώς στο μηδέν εάν μειώσετε τη συχνότητα της γεννήτριας με κάποιο τρόπο. Η μείωση της συχνότητας θα έχει ως αποτέλεσμα τη μείωση του EMF αυτοεπαγωγής και συνεπώς τη μείωση της μετατόπισης φάσης μεταξύ του ρεύματος και της τάσης στο κύκλωμα που προκαλείται από αυτό.

Η ισχύς ενός κυκλώματος AC που περιέχει επαγωγέα

Το κύκλωμα εναλλασσόμενου ρεύματος που περιέχει το πηνίο δεν καταναλώνει την ενέργεια της πηγής ρεύματος και ότι στο κύκλωμα υπάρχει μια διαδικασία ανταλλαγής ενέργειας μεταξύ της γεννήτριας και του κυκλώματος.

Ας αναλύσουμε τώρα πώς θα είναι τα πράγματα με την ισχύ που καταναλώνει ένα τέτοιο σχήμα.

Η ισχύς που καταναλώνεται σε ένα κύκλωμα AC είναι ίση με το γινόμενο του ρεύματος και της τάσης, αλλά επειδή το ρεύμα και η τάση είναι μεταβλητά μεγέθη, τότε η ισχύς θα είναι επίσης μεταβλητή.Σε αυτήν την περίπτωση, μπορούμε να προσδιορίσουμε την τιμή ισχύος για κάθε χρονική στιγμή αν πολλαπλασιάσουμε την τιμή ρεύματος με την τιμή τάσης που αντιστοιχεί σε μια δεδομένη χρονική στιγμή.

Για να λάβουμε το γράφημα ισχύος, πρέπει να πολλαπλασιάσουμε τις τιμές των ευθύγραμμων τμημάτων που ορίζουν το ρεύμα και την τάση σε διαφορετικούς χρόνους. Μια τέτοια κατασκευή φαίνεται στο σχ. 3, α. Η διακεκομμένη κυματομορφή p μας δείχνει πώς αλλάζει η ισχύς σε ένα κύκλωμα AC που περιέχει μόνο επαγωγική αντίσταση.

Για την κατασκευή αυτής της καμπύλης χρησιμοποιήθηκε ο ακόλουθος αλγεβρικός κανόνας πολλαπλασιασμού: Όταν μια θετική τιμή πολλαπλασιάζεται με μια αρνητική τιμή, προκύπτει μια αρνητική τιμή και όταν πολλαπλασιάζονται δύο αρνητικές ή δύο θετικές τιμές, προκύπτει μια θετική τιμή.

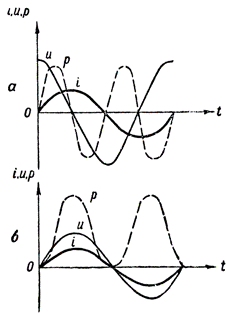
Σχήμα 3. Γραφήματα ισχύος: α — σε ένα κύκλωμα που περιέχει επαγωγική αντίσταση, β — επίσης, ενεργή αντίσταση

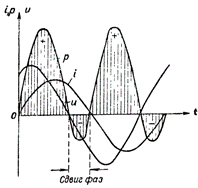
Εικόνα 4. Διάγραμμα ισχύος για ένα κύκλωμα που περιέχει R και L.

Η καμπύλη ισχύος σε αυτή την περίπτωση βρίσκεται πάνω από τον άξονα του χρόνου. Αυτό σημαίνει ότι δεν υπάρχει ανταλλαγή ενέργειας μεταξύ της γεννήτριας και του κυκλώματος και επομένως η ισχύς που παρέχεται από τη γεννήτρια στο κύκλωμα καταναλώνεται πλήρως από το κύκλωμα.

Στο σχ. Το σχήμα 4 δείχνει το διάγραμμα ισχύος για ένα κύκλωμα που περιέχει και επαγωγική και ενεργή αντίσταση. Σε αυτή την περίπτωση, συμβαίνει επίσης η αντίστροφη μεταφορά ενέργειας από το κύκλωμα στην πηγή ρεύματος, αλλά σε πολύ μικρότερο βαθμό από ό,τι σε ένα κύκλωμα με μία μόνο επαγωγική αντίσταση.

Αφού εξετάσουμε τα παραπάνω γραφήματα ισχύος, συμπεραίνουμε ότι μόνο η μετατόπιση φάσης μεταξύ ρεύματος και τάσης στο κύκλωμα δημιουργεί «αρνητική» ισχύ.Σε αυτή την περίπτωση, όσο μεγαλύτερη είναι η μετατόπιση φάσης μεταξύ του ρεύματος και της τάσης στο κύκλωμα, τόσο λιγότερη ισχύς θα καταναλώνεται από το κύκλωμα, και αντίστροφα, όσο μικρότερη είναι η μετατόπιση φάσης, τόσο μεγαλύτερη είναι η ισχύς που καταναλώνεται από το κύκλωμα.

Διαβάστε επίσης: Τι είναι ο συντονισμός τάσης